Colles PC* 2016-2017
Compléments d'algèbre linéaire, séries numériques
Dans toute cette partie,  désigne
désigne
 ou
ou
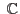 .
.
Le programme est organisé autour de trois objectifs :
- consolider les acquis de la classe de première année ;
- étudier de nouveaux concepts : somme de plusieurs sous-espaces vectoriels, sous-espaces stables, trace ;
- passer du registre géométrique au registre matriciel et inversement.
Le programme valorise les interprétations géométriques et l'illustration des notions et des résultats par de nombreuses figures.

Cette partie consolide et élargit les acquis de première année sur les séries, notamment la convergence absolue, en vue de l'étude des probabilités discrètes et des séries de fonctions.
La semi-convergence n'est pas un objectif du programme.

Les étudiants sauront redémontrer les différents résultats du cours.Il est opportun de revoir :
- La fiche sur les limites et équivalents usuels;
- Le chapitre de sup sur les suites;
- Le chapitre de sup sur les séries.
- Le chapitre de sup sur les développements limités.
Quelques documents pour l'année :
Documents :
O-O-O-O-O-O-O-O-O-O-O-O
Réduction des endomorphismes
Après avoir introduit le vocabulaire des éléments propres en dimension quelconque, cette partie s'intéresse de manière plus approfondie au cas de la dimension finie, et à la question de diagonalisabilité d'une matrice carrée.
L'application des résultats de la réduction à la recherche des solutions d'une récurrence linéaire à coefficients constants crée un nouveau pont entre l'algèbre et l'analyse et anticipe l'étude des équations différentielles linéaires, dont la résolution repose sur des outils similaires.
La notion de polynôme annulateur est hors programme. L'étude des classes de similitude est hors programme.

Les étudiants profiteront de ce chapitre pour très opportunément réviser :
- Le chapitre 1 sur les compléments d'algèbre linéaire;
- Les chapitres de sup d'algèbre linéaire :
Documents :
O-O-O-O-O-O-O-O-O-O-O-O
Intégrales sur un intervalle
L'objectif de ce chapitre est multiple :
- étendre la notion d'intégrale étudiée en première année à des fonctions continues par morceaux sur un intervalle quelconque par le biais des intégrales généralisées ;
- définir, dans le cadre des fonctions continues par morceaux, la notion de fonction intégrable ;
- compléter le chapitre dédié aux suites et aux séries de fonctions par le théorème de la convergence dominée et le théorème d'intégration terme à terme ;
- étudier les fonctions définies par des intégrales dépendant d'un paramètre.
Les fonctions considérées sont définies sur un intervalle de
 et à valeurs réelles ou complexes.
et à valeurs réelles ou complexes.

Les étudiants profiteront de ce chapitre pour très opportunément réviser :
- Les limites et équivalents usuels;
- Les primitives et dérivées des fonctions usuelles.
- Le chapitre de sup d'intégration et en particulier :
- Le théorème fondamental de l'analyse;
- Les sommes de Riemann;
- Les différentes techniques de calcul de primitive.
Documents :
O-O-O-O-O-O-O-O-O-O-O-O
Ce chapitre vise les objectifs suivants :
- généraliser au cas des espaces vectoriels de dimension finie sur
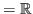 ou
ou
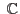 certaines notions (convergence de suites, limite et continuité de fonctions) étudiées en première année dans le cadre de l'analyse réelle, indispensables pour aborder l'étude des suites de matrices, des fonctions à valeurs vectorielles et du calcul différentiel ;
certaines notions (convergence de suites, limite et continuité de fonctions) étudiées en première année dans le cadre de l'analyse réelle, indispensables pour aborder l'étude des suites de matrices, des fonctions à valeurs vectorielles et du calcul différentiel ;
- préparer l'introduction de la norme de la convergence uniforme, afin de fournir un cadre topologique à la convergence des suites et séries de fonctions.
L'aspect géométrique de certains concepts topologiques gagne à être illustré par de nombreuses figures.

Les étudiants profiteront de ce chapitre pour très opportunément réviser :
- La notion de borne supérieure;
- L'axiome de la borne supérieure;
- Le théorème de caractérisation de la borne supérieure et sa traduction en terme de point adhérent;
- Le chapitre de sup sur les limites de suites et de fonctions.
Documents :
O-O-O-O-O-O-O-O-O-O-O-O
L'objectif de ce chapitre est de définir les modes usuels de convergence d'une suite et d'une série de fonctions et de les exploiter pour étudier la stabilité des propriétés de ces fonctions par passage à la limite. En prolongement du chapitre sur les espaces vectoriels normés de dimension finie, un lien est établi avec l'utilisation de la norme de la convergence uniforme.
Les fonctions sont définies sur un intervalle 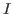 de
de
 et à valeurs dans
et à valeurs dans
 ou
ou
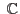 .
.
Les étudiants profiteront de ce chapitre pour très opportunément réviser :
- Le chapitre sur les intégrales généralisées
- Le chapitre sur les séries numériques.
- La fiche de synthèse sur les inégalités classiques ci-dessous.
On s'assurera en particulier que les élèves maîtrisent les encadrement pour les restes et les sommes partielles d'une série alternée satisfaisant les hypothèses du critère spécial et les comparaisons séries-intégrales.
Documents :
O-O-O-O-O-O-O-O-O-O-O-O
Les objectifs de ce chapitre sont les suivants :
- étudier la convergence d'une série entière de variable complexe et mettre en évidence la notion de rayon de convergence ;
- étudier les propriétés de sa somme en se limitant à la continuité dans le cas d'une variable complexe ;
- établir les développements en série entière des fonctions usuelles.
La théorie des séries entières sera appliquée au cas des séries génératrices dans le chapitre dédié aux variables aléatoires discrètes et à la recherche de solutions d'équations différentielles linéaires.

- Les développements en séries entières des fonctions usuelles seront connus et les élèves sauront les retrouver.
- Les étudiants sauront utiliser une équation différentielle ou une équation fonctionnelle pour calculer un DSE.
- Ils sauront aussi utiliser les séries entières pour calculer la somme d'une série.
- Les liens entre séries numériques, séries de fonctions et séries entières devront être parfaitement établis.
- Le cours devra être parfaitement maîtrisé.
Documents :
O-O-O-O-O-O-O-O-O-O-O-O
Cette partie a pour objectif la mise en place du cadre général de la théorie des probabilités permettant d'aborder l'étude de processus stochastiques à temps discret. Cette mise en place se veut minimale. En particulier :
- la notion de tribu ne doit donner lieu à aucun développement théorique autre que sa définition ;
- la construction d'espaces probabilisés n'est pas un objectif du programme.

- Les démonstrations des différentes formules du cours seront parfaitement maîtrisées.
- Les étudiants savent modéliser l'expérience aléatoire consistant à jeter une infinité de fois un dé ou une pièce de monnaie.
- Ils réviseront opportunément la résolution des récurrences linéaires d'ordres 1, 2 et plus.
Documents :
O-O-O-O-O-O-O-O-O-O-O-O
Les objectifs de cette partie sont les suivants :
- étendre la notion de variable aléatoire finie à des variables dont l'image est un ensemble dénombrable ;
- fournir des outils permettant, sur des exemples simples, l'étude de processus stochastiques à temps discret ;
- exposer deux résultats asymptotiques : l'approximation de la loi binomiale par la loi de Poisson et la loi faible des grands nombres ;
- introduire les fonctions génératrices et utiliser les propriétés des séries entières.
La construction d'espaces probabilisés modélisant une suite d'expériences aléatoires est hors programme, on admet l'existence de tels espaces. Les différents types de convergence probabiliste (presque sûre, en probabilité, en loi, en moyenne) sont hors programme.
Toutes les variables aléatoires mentionnées dans le programme sont implicitement supposées discrètes.

- Les démonstrations des différents résultats du cours seront parfaitement maîtrisées.
- Les étudiants sauront faire bon usage des différentes lois usuelles
- Le chapitre sur les espaces probabilisables est naturellement à revoir.
- Il sera tout à fait opportun de revoir aussi le chapitre sur les séries numériques et le chapitre sur les séries entières.
- Les techniques de résolution des récurrences linéaires seront aussi reprises.
Documents :
O-O-O-O-O-O-O-O-O-O-O-O
Ce chapitre est organisé autour de trois objectifs :
- consolider les acquis de la classe de première année sur les espaces euclidiens ;
- étudier les isométries vectorielles et les matrices orthogonales, et les classifier en dimension deux en insistant sur les représentations géométriques ;
- énoncer les formes géométrique et matricielle du théorème spectral.

- Les démonstrations des différents résultats du cours seront parfaitement maîtrisés.
- Les étudiants sauront reconnaître des projecteurs orthogonaux et des symétries orthogonales, ainsi que en dimension
 des rotations et des réflexions.
des rotations et des réflexions.
- Ils sauront utiliser les projections orthogonales dans des problèmes de meilleur approximation.
- Ils sauront aussi redémontrer l'inégalité de Cauchy-Schwarz et l'appliquer à la mise en place d'inégalités.
Documents :
O-O-O-O-O-O-O-O-O-O-O-O
Révisions: toute l'année :
- Compléments d'algèbre linéaire
- Séries numériques
- Réduction des endomorphismes
- Intégrales généralisées
- Espaces vectoriels normés
- Suites et séries de fonctions
- Séries entières
- Espaces probabilisés
- Variables aléatoires discrètes
- Espaces euclidiens et préhilbertien
- Fonctions à valeurs vectorielles
- Equations différentielles
Programme officiel pour les deux derniers chapitres :
L'objectif de ce chapitre est double :
- généraliser aux fonctions à valeurs dans
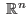 la notion de dérivée d'une fonction numérique, en vue notamment de préparer le chapitre sur les équations différentielles ;
la notion de dérivée d'une fonction numérique, en vue notamment de préparer le chapitre sur les équations différentielles ;
- formaliser des notions géométriques (arc paramétré, tangente) et cinématiques (vitesse, accélération) rencontrées dans d'autres disciplines scientifiques.
Toutes les fonctions sont définies sur un intervalle 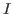 de
de
 et à valeurs dans
et à valeurs dans
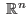 .
.

L'étude des équations différentielles linéaires scalaires d'ordres un et deux, abordée en première année, se poursuit par celle des systèmes
différentiels linéaires d'ordre  et des équations scalaires à coefficients non constants, en mettant l'accent sur les équations d'ordre deux. On
s'attache à développer à la fois les aspects théorique et pratique :
et des équations scalaires à coefficients non constants, en mettant l'accent sur les équations d'ordre deux. On
s'attache à développer à la fois les aspects théorique et pratique :
- la forme des solutions ;
- le théorème de Cauchy linéaire ;
- le lien entre les équations scalaires et les systèmes différentiels d'ordre un ;
- la résolution explicite.
Ce chapitre favorise les interactions avec les autres disciplines scientifiques.
Dans tout ce chapitre,  désigne
désigne
 ou
ou
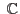 et
et 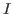 est un intervalle de
est un intervalle de
 .
.

Documents :
O-O-O-O-O-O-O-O-O-O-O-O
Colles PC* 2016-2017
This document was generated using the
LaTeX2HTML translator Version 2008 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -local_icons -no_footnode -no_navigation -split 0 /home/manu/TSI/2016_2017/Pages_spe/trimestre1.tex
The translation was initiated by manu on 2017-03-08
manu
2017-03-08
![]() désigne
désigne
![]() ou
ou
![]() .
.



![]() et à valeurs réelles ou complexes.
et à valeurs réelles ou complexes.


![]() de
de
![]() et à valeurs dans
et à valeurs dans
![]() ou
ou
![]() .
.
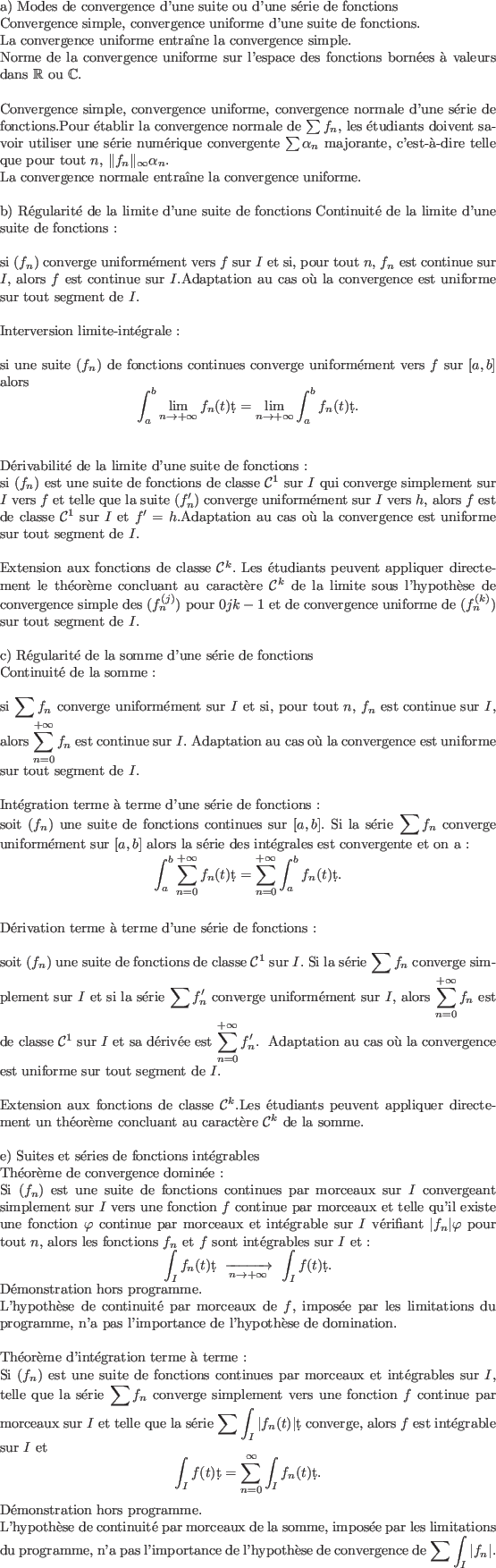





![]() et des équations scalaires à coefficients non constants, en mettant l'accent sur les équations d'ordre deux. On
s'attache à développer à la fois les aspects théorique et pratique :
et des équations scalaires à coefficients non constants, en mettant l'accent sur les équations d'ordre deux. On
s'attache à développer à la fois les aspects théorique et pratique :
![]() désigne
désigne
![]() ou
ou
![]() et
et ![]() est un intervalle de
est un intervalle de
![]() .
.
