


suivant: Théorèmes d'isomorphie
monter: Groupes quotients
précédent: Construction du quotient d'un
Remarque Si x est élément de G, nous noterons  la classe d'équivalence de x dans G/H
la classe d'équivalence de x dans G/H . x sera alors un représentant de la classe
d'équivalence
. x sera alors un représentant de la classe
d'équivalence  .
.
Définition Nous allons définir une loi interne 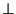
 sur G/H
sur G/H  par: Si x et y sont éléments de G alors
par: Si x et y sont éléments de G alors
Quand aucune confusion n'est à craindre, nous noterons la loi interne de G/H de la même façon que celle de G. Cette loi est celle induite de G sur
G/H.
Remarque Il faut vérifier que cette loi est bien définie sur G/H, c.a.d que si x,x',y,y' sont des éléments de G tels que
Proposition La loi définie précédemment est bien définie si et seulement si H est normal dans G.
Démonstration La condition à vérifier pour que la loi précédente soit bien définie sur G/H est que si x,x',y,y' sont des éléments de G tels que
Etudions quelle propriété sur H nous permet de
valider cette condition. La condition précédente est équivalente à la suivante:
Mais comme, par hypothèse, 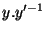 est élément de H
est élément de H  et que tout élément de H peut s'écrire sous la forme
et que tout élément de H peut s'écrire sous la forme 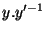 où y est élément
de G ( si h est dans H on écrit h=h.
où y est élément
de G ( si h est dans H on écrit h=h.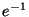 !!!), cette condition implique la suivante (qui semble bien moins restrictive):
!!!), cette condition implique la suivante (qui semble bien moins restrictive):
ou, autrement dit, notre condition de départ entraîne celle que H est normal dans G . Résumons nous: La loi définie
précédemment sur G/H nous assure d'une structure de groupe sur cet ensemble seulement si H est normal dans G. Montrons que cette condition est aussi
suffisante: Supposons alors que H est normal dans G. Si
. Résumons nous: La loi définie
précédemment sur G/H nous assure d'une structure de groupe sur cet ensemble seulement si H est normal dans G. Montrons que cette condition est aussi
suffisante: Supposons alors que H est normal dans G. Si
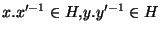 , montrons alors que
, montrons alors que
 Notons
Notons
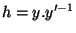 .
. 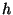 est élément de h. Il faut donc montrer que
est élément de h. Il faut donc montrer que 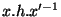 est élément de H. Mais on peut écrire:
est élément de H. Mais on peut écrire:
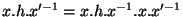 et comme H est normal dans G et que
et comme H est normal dans G et que
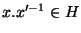 alors
alors 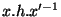 est bien élément de H comme produit
d'éléments de H.
est bien élément de H comme produit
d'éléments de H.
Théorème fondamental Supposons que H est un sous groupe normal de G. L'ensemble G/H
de G. L'ensemble G/H  muni de la loi interne induite
muni de la loi interne induite  de celle de G a une structure de groupe. De plus, si G est abélien
de celle de G a une structure de groupe. De plus, si G est abélien  il en est de même de G/H équipé de la loi induite.
il en est de même de G/H équipé de la loi induite.
Démonstration Comme H est normal dans G la loi induite
dans G la loi induite par celle de G sur G/H est bien définie.
par celle de G sur G/H est bien définie.
L'élément 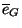 est le neutre de la loi . Dans G/H:
est le neutre de la loi . Dans G/H:
De plus tout élément de G/H  possède un inverse qui est
possède un inverse qui est
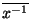 . (Donc
. (Donc
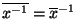 ).
L'associativité de la loi induite se démontre en passant au quotient celle de la loi de départ. De même, on démontrerait que la loi induite est
commutative si la loi de départ l'est aussi, et donc que G/H est abélien si G l'est.
).
L'associativité de la loi induite se démontre en passant au quotient celle de la loi de départ. De même, on démontrerait que la loi induite est
commutative si la loi de départ l'est aussi, et donc que G/H est abélien si G l'est.



suivant: Théorèmes d'isomorphie
monter: Groupes quotients
précédent: Construction du quotient d'un
Emmanuel_Vieillard-Baron_pour_les.mathematiques