


suivant: Quelques définitions supplémentaires
monter: Groupes quotients
précédent: Structure de l'ensemble quotient
Proposition Supposons que
 . Notons
. Notons

 l'application qui à
l'application qui à  associe sa classe d'équivalence
associe sa classe d'équivalence 
 dans G/H. Alors
dans G/H. Alors  est un homomorphisme de groupe
est un homomorphisme de groupe . De plus H=Ker
. De plus H=Ker 
 et
et  est surjectif.
est surjectif.
Démonstration Soient x et y des éléments de G alors
Cette propriété n'est que
l'expression de la définition de la loi de groupe sur G/H. Pour l'égalité entre le noyau de  et H, il suffit de remarquer que tout élément de
H est équivalent dans G/H au neutre de G/H. De plus si
et H, il suffit de remarquer que tout élément de
H est équivalent dans G/H au neutre de G/H. De plus si  est un élément de G/H, x est un antécédent de cet élément par
est un élément de G/H, x est un antécédent de cet élément par  . Donc
. Donc  est bien surjectif.
est bien surjectif.
Théorème Premier théorème d'isomorphisme Soient G et G' des groupes. Soit
 un homomorphisme de groupe
un homomorphisme de groupe . Rappelons que Ker
. Rappelons que Ker  est un sous groupe distingué de G
est un sous groupe distingué de G  et donc que G/Ker
et donc que G/Ker  a une structure de groupe pour la loi induite de celle de G
a une structure de groupe pour la loi induite de celle de G . Rappelons aussi que l'on a un morphisme surjectif
. Rappelons aussi que l'on a un morphisme surjectif
 qui a tout élément de G associe sa classe d'équivalence dans G/Ker
qui a tout élément de G associe sa classe d'équivalence dans G/Ker 
 . Ajoutons encore que l'image d'un groupe par un morphisme est un sous groupe du groupe image. On peut alors affirmer qu'il existe un isomorphisme
. Ajoutons encore que l'image d'un groupe par un morphisme est un sous groupe du groupe image. On peut alors affirmer qu'il existe un isomorphisme 
 tel que
tel que
 .
.
Démonstration Posons H=Ker  .
.
Construisons tout d'abord  . Posons, si
. Posons, si
 ,
,
 où x est un représentant de la classe
d'équivalence
où x est un représentant de la classe
d'équivalence  .
.  est bien définie car si y est un autre représentant de la classe d'équivalence associée à x, alors
est bien définie car si y est un autre représentant de la classe d'équivalence associée à x, alors
 . Cette dernière égalité est vraie car
. Cette dernière égalité est vraie car  est un morphisme et x et y étant équivalents dans G/H,
est un morphisme et x et y étant équivalents dans G/H, 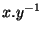 est élément de Ker
est élément de Ker  . Donc
. Donc  et
et  est bien définie.
est bien définie.
 est bien ,par définition ,un homomorphisme de groupe
est bien ,par définition ,un homomorphisme de groupe .
.
Montrons que  est injective. Soient
est injective. Soient
 . Supposons que
. Supposons que
 alors par définition de
alors par définition de  , on a:
, on a:  donc
donc
 et comme
et comme  est un homomorphisme,
est un homomorphisme,
 . Ce qui implique que
. Ce qui implique que

 et donc que
et donc que
 . Ceci prouve l'injectivité de
. Ceci prouve l'injectivité de  .
.
Comme une application est surjective sur son image (!!!)  est un isomorphisme
est un isomorphisme de G/H dans Im
de G/H dans Im  .
Enfin par définition de
.
Enfin par définition de  on a bien
on a bien
 .
.
Théorème Second théorème d'isomorphisme Soient G un groupe, H et K des sous groupes de G. On suppose que H G
G . Alors H
. Alors H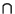 K est normal dans K
K est normal dans K  et K/(K
et K/(K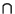 G)
G) HK/H
HK/H .
.
Démonstration
- Montrons que H
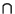 K est normal dans G
K est normal dans G . Il est tout d'abord évident que H
. Il est tout d'abord évident que H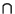 K est un sous groupe de G (Une intersection de sous-groupes
est encore un sous-groupe). Soit x un élément de H
K est un sous groupe de G (Une intersection de sous-groupes
est encore un sous-groupe). Soit x un élément de H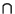 K et soit
K et soit 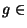 K. Alors
K. Alors  est, comme H est normal dans G, encore élément de H.
est, comme H est normal dans G, encore élément de H.
 est aussi élément de K comme produit d'élément de K. Donc
est aussi élément de K comme produit d'élément de K. Donc  est bien élément de H
est bien élément de H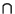 K et H
K et H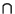 K est bien distingué dans
K.
K est bien distingué dans
K.
- Remarquons maintenant que HK est un sous groupe de G pour la loi induite de celle de G. L'élément neutre de G est naturellement élément de HK. Et si g=h.k, g'=h'.k' sont des éléments de HK alors
Comme H est normal dans G, k.h'.k est élément de H et donc égal à un élément h'' de H
est élément de H et donc égal à un élément h'' de H . Donc g.g'=h.h''.k
. Donc g.g'=h.h''.k .k' est bien de la forme d'un produit d'un élément de H et d'un élément de K. Notre loi est donc bien interne
.k' est bien de la forme d'un produit d'un élément de H et d'un élément de K. Notre loi est donc bien interne . Enfin, si g=h.k alors g
. Enfin, si g=h.k alors g =k
=k .h
.h =k
=k .h
.h .k.k
.k.k . Comme H est normal dans G,k
. Comme H est normal dans G,k .h
.h .k est élément de H et l'inverse de g est bien élément de HK.
.k est élément de H et l'inverse de g est bien élément de HK.
- H
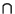 K étant normal dans K
K étant normal dans K , K/(K
, K/(K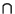 G) a une structure de groupe pour la loi induite de celle de K
G) a une structure de groupe pour la loi induite de celle de K . Montrons que ce groupe est isomorphe à HK/K
. Montrons que ce groupe est isomorphe à HK/K . Définissons pour cela l'application
. Définissons pour cela l'application
 par si g=h.k est élément de HK,
par si g=h.k est élément de HK,
 où
où  désigne la classe d'équivalence de h dans
désigne la classe d'équivalence de h dans  . Cette application est bien définie car si g est aussi représenté par le produit h'.k' de HK alors h.k=h'.k' et k.k'
. Cette application est bien définie car si g est aussi représenté par le produit h'.k' de HK alors h.k=h'.k' et k.k' =h
=h .h'. Le
produit du second membre de l'égalité est élément de H et le produit du premier membre élément de K. On en déduit que h.h'
.h'. Le
produit du second membre de l'égalité est élément de H et le produit du premier membre élément de K. On en déduit que h.h' est élément de
est élément de
 . Donc
. Donc
 et
et
 .
.
Comme  est un sous groupe normal de H alors l'application
est un sous groupe normal de H alors l'application  ( qui à un élément de HK associe sa classe d'équivalence...) est un homomorphisme de groupe
( qui à un élément de HK associe sa classe d'équivalence...) est un homomorphisme de groupe .
.
- Calculons alors Ker(
 )
) . Soit g=h.k
. Soit g=h.k tel que
tel que
 . h est donc élément de
. h est donc élément de  . Par conséquent g est un produit de deux éléments de K et est élément de K. On vient d'établir Ker
. Par conséquent g est un produit de deux éléments de K et est élément de K. On vient d'établir Ker
 K. Prenons un élément k de K. Par définition de
K. Prenons un élément k de K. Par définition de  ,
,  (k)=
(k)= . Ceci prouve l'inclusion réciproque. En conclusion: Ker
. Ceci prouve l'inclusion réciproque. En conclusion: Ker =K.
=K.
 est surjective. En effet, si
est surjective. En effet, si  est élément de
est élément de 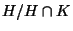 alors
alors  (h)=
(h)= .
.
- Appliquons enfin le premier théorème d'isomorphisme
 à
à  :
:
 .
.

Théorème Troisième théorème d'isomorphisme Soient G un groupe, H et K des sous groupes de G. On suppose que H G et que K
G et que K
 G
G . On suppose de plus que H
. On suppose de plus que H K. Alors K/H
K. Alors K/H G/H et
G/H et
Démonstration
Soit g un élément de G. Notons  sa classe d'équivalence dans G/H et
sa classe d'équivalence dans G/H et
 sa classe d'équivalence dans G/K
sa classe d'équivalence dans G/K .
.
Montrons que K/H G/H. Pour cela choisissons un élément
G/H. Pour cela choisissons un élément  dans G/H et une élément
dans G/H et une élément  dans K/H. Alors
dans K/H. Alors
 . Mais K étant normal dans G
. Mais K étant normal dans G , il existe k'
, il existe k' K tel que ce dernier élément soit égal à
K tel que ce dernier élément soit égal à  , Cqfd.
, Cqfd.
Soit  l'application qui à un élément
l'application qui à un élément  de G/H associe l'élément
de G/H associe l'élément
 de G/K.
de G/K.  est bien définie et est un morphisme du groupe G/H dans le groupe G/K
est bien définie et est un morphisme du groupe G/H dans le groupe G/K . De plus, H étant inclu dans K,
. De plus, H étant inclu dans K,  est surjective. On peut alors appliquer le premier théorème d'isomorphisme
est surjective. On peut alors appliquer le premier théorème d'isomorphisme . Ceci nous permet d'affirmer que
. Ceci nous permet d'affirmer que



suivant: Quelques définitions supplémentaires
monter: Groupes quotients
précédent: Structure de l'ensemble quotient
Emmanuel_Vieillard-Baron_pour_les.mathematiques
![]() sa classe d'équivalence dans G/H et
sa classe d'équivalence dans G/H et
![]() sa classe d'équivalence dans G/K
sa classe d'équivalence dans G/K![]() .
.
![]() G/H. Pour cela choisissons un élément
G/H. Pour cela choisissons un élément ![]() dans G/H et une élément
dans G/H et une élément ![]() dans K/H. Alors
dans K/H. Alors
![]() . Mais K étant normal dans G
. Mais K étant normal dans G![]() , il existe k'
, il existe k'![]() K tel que ce dernier élément soit égal à
K tel que ce dernier élément soit égal à ![]() , Cqfd.
, Cqfd.
![]() l'application qui à un élément
l'application qui à un élément ![]() de G/H associe l'élément
de G/H associe l'élément
![]() de G/K.
de G/K. ![]() est bien définie et est un morphisme du groupe G/H dans le groupe G/K
est bien définie et est un morphisme du groupe G/H dans le groupe G/K![]() . De plus, H étant inclu dans K,
. De plus, H étant inclu dans K, ![]() est surjective. On peut alors appliquer le premier théorème d'isomorphisme
est surjective. On peut alors appliquer le premier théorème d'isomorphisme![]() . Ceci nous permet d'affirmer que
. Ceci nous permet d'affirmer que