


suivant: Structure de l'ensemble quotient
monter: Groupes quotients
précédent: Introduction
Dans toute cette leçon, (G,.) désigne un groupe et (H,.) désigne un sous groupe de G. On considère aussi la relation, si x et y sont éléments
de G:
Proposition La relation 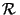 définie par
définie par
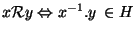 est une relation d'équivalence
est une relation d'équivalence .
.
Démonstration Triviale!!
Définition On notera 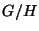 l'ensemble
l'ensemble 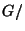
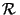 des classes d'équivalences
des classes d'équivalences  de la relation
de la relation 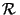 sur G.
sur G.
Proposition Soit  . La classe d'équivalence de x
. La classe d'équivalence de x  pour la relation
pour la relation
est l'ensemble
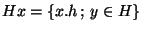 .
.
Démonstration Soit 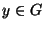 équivalent à x pour la relation
équivalent à x pour la relation 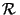 . Alors il existe
. Alors il existe 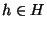 tel que
tel que 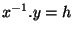 . Et donc y est élément de
. Et donc y est élément de 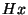 .
Réciproquement, si y est élémennt de
.
Réciproquement, si y est élémennt de 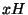 , il est clair que y
, il est clair que y 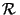 x.
x.
Définition L'ensemble 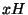 s'appelle classe à gauche de l'élément x de G.
s'appelle classe à gauche de l'élément x de G.
Remarque On aurait aussi put définir notre relation d'équivalence 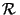 par:
par:
Dans ce cas, la classe d'équivalence d'un élément x de G aurait été donné par l'ensemble 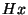 .
.
Définition L'ensemble 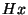 s'appelle classe à droite de l'élément x de G.
s'appelle classe à droite de l'élément x de G.
Proposition Si H est un sous groupe fini
fini de G et si x et y sont deux éléments de G alors les classes d'équivalences (à gauche ou à droite) de x et y pour
la relation
de G et si x et y sont deux éléments de G alors les classes d'équivalences (à gauche ou à droite) de x et y pour
la relation 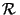 ont même nombre d'éléments et ce nombre est égal au cardinal de H.
ont même nombre d'éléments et ce nombre est égal au cardinal de H.
Démonstration Soit x un élément de G. Posons
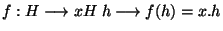 .
.  est injective car si h et h' sont des éléments de H
tels que
est injective car si h et h' sont des éléments de H
tels que 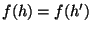 alors on a l'égalité
alors on a l'égalité 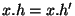 et x étant élément du groupe G, ceci implique, en multipliant à gauche chacun des membres de
l'égalité précédente par
et x étant élément du groupe G, ceci implique, en multipliant à gauche chacun des membres de
l'égalité précédente par 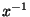 que h=h'.
que h=h'.  est aussi surjective car si y est un élément de xH, alors il existe
est aussi surjective car si y est un élément de xH, alors il existe 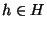 tel que
tel que 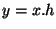 et donc
et donc
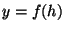 . f étant à la fois injective et surjective, elle est bijective. Ceci prouve que H et xH ont même nombre d'éléments. Mais si y est un élément de G, yH et H auront aussi même nombre d'éléments. Donc xH et yH ont même cardinal.
. f étant à la fois injective et surjective, elle est bijective. Ceci prouve que H et xH ont même nombre d'éléments. Mais si y est un élément de G, yH et H auront aussi même nombre d'éléments. Donc xH et yH ont même cardinal.
De même on montrerait que toutes les classes à droite pour une relation 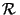 , issue d'un sous groupe H de cardinal fini dans G, ont même nombre
d'éléments, ce nombre étant égal à |H|.
, issue d'un sous groupe H de cardinal fini dans G, ont même nombre
d'éléments, ce nombre étant égal à |H|.
Le théorème qui vient maintenant et qui résulte des propositions précédentes est fondamental en algèbre.
Théorème de Lagrange Soit G un groupe fini. Si H est un sous groupe de G, alors le cardinal de H divise celui de G. On notera |G/H| où [G:H] le nombre
|G|/|H|. [G:H] s'appelle l'indice de H dans G.
Démonstration Soit donc H un sous groupe de G. On considère la relation d'équivalence 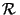 associée à H. Elle nous permet de définir une partition de G par
des sous ensembles de la forme xH où
associée à H. Elle nous permet de définir une partition de G par
des sous ensembles de la forme xH où  . On peut donc trouver, G étant fini, un nombre
. On peut donc trouver, G étant fini, un nombre
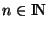 et
et
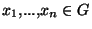 tels que
tels que
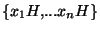 forme une partition de G. Mais les sous ensembles
forme une partition de G. Mais les sous ensembles 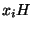 ont tous, d'après la proposition précédente
ont tous, d'après la proposition précédente , le même nombre
d'éléments. De plus, ce nombre est égale à |H|. Donc le cardinal de G s'écrit |G|=n|H|. Ceci prouve notre théorème.
, le même nombre
d'éléments. De plus, ce nombre est égale à |H|. Donc le cardinal de G s'écrit |G|=n|H|. Ceci prouve notre théorème.
On donne maintenant un corollaire du théorème de Lagrange qui est absolument fondamental dans la théorie des groupes finis.
Théorème Soit G un groupe. Soit g un élément de G d'ordre fini . Alors l'ordre de g
. Alors l'ordre de g  divise l'ordre de G
divise l'ordre de G .
.
Démonstration Soient G et g comme dans l'énoncé du théorème et soit n l'ordre de g . Alors
. Alors
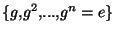 est un sous groupe de G
est un sous groupe de G . Cette affirmation est triviale à vérifier. De plus, par définition de l'ordre d'un élément dans un groupe
. Cette affirmation est triviale à vérifier. De plus, par définition de l'ordre d'un élément dans un groupe , ce sous groupe est de cardinal n. Par application du théorème de Lagrange
, ce sous groupe est de cardinal n. Par application du théorème de Lagrange , n est un diviseur du cardinal de G.
, n est un diviseur du cardinal de G.
On se posera, un peu plus tard dans le cours, le problème réciproque, à savoir: Si p est un diviseur de l'ordre du groupe  alors existe-t-il un élément d'ordre p
alors existe-t-il un élément d'ordre p  dans G ou encore: existe-t-il un sous groupe d'ordre p dans G. La réponse sera donnée par le théorème de Cauchy
dans G ou encore: existe-t-il un sous groupe d'ordre p dans G. La réponse sera donnée par le théorème de Cauchy  pour les éléments d'ordre p et sous certaines conditions sur p, et par le théorème de Sylows
pour les éléments d'ordre p et sous certaines conditions sur p, et par le théorème de Sylows , pour les sous groupes d'ordre p, sous certaines conditions sur p et sur G.
, pour les sous groupes d'ordre p, sous certaines conditions sur p et sur G.
Il est naturel de se demander pour quelles conditions sur H on a coïncidence entre les classes à gauche  et les classes à droite
et les classes à droite . Nous allons nous
pencher sur cette question dans la fin de ce paragraphe.
. Nous allons nous
pencher sur cette question dans la fin de ce paragraphe.
Définition On dira que le sous groupe H de G est distingué ou normal dans G si pour tout g dans G et tout h dans H on a:
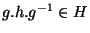 . On
note
. On
note
 le fait que H soit normal dans G.
le fait que H soit normal dans G.
Proposition Soit donc H un sous groupe de groupe G. Les classes à gauche et à droite de la relation d'équivalence héritée de H coïncident si et seulement
si H est normal dans G.
Démonstration Supposons que les classes à gauche et à droite coïncident. Pour tout g dans G, on a: gH=Hg. donc en particulier, pour tout h dans H, il existe
h' dans H tel que g.h=h'.g. Donc pour tout h dans H, il existe h' tel que g.h.g =h'
=h'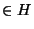 . Ceci prouve que
. Ceci prouve que
 .
.
Réciproquement, supposons que
 . Alors pour tout g dans G et tout h dans H, g.h.g
. Alors pour tout g dans G et tout h dans H, g.h.g est élément de H. Donc pour tout g dans
G et tout h dans H, g.h est dans H.g. On a ainsi montré que pour tout élément g de G, gH
est élément de H. Donc pour tout g dans
G et tout h dans H, g.h est dans H.g. On a ainsi montré que pour tout élément g de G, gH Hg. Comme les cardinaux de gH et Hg sont égaux à
celui de H, ils sont égaux entre eux et on a alors bien gH=Hg.
Hg. Comme les cardinaux de gH et Hg sont égaux à
celui de H, ils sont égaux entre eux et on a alors bien gH=Hg.
La proposition suivante semble être anecdotique alors qu'elle est en fait fondamentale et permet de construire des groupes parmi les plus importants
en Mathématique.
Proposition Si G et G' sont deux groupes et que
 est un homomorphisme de groupe
est un homomorphisme de groupe  alors le noyau de
alors le noyau de  : Ker
: Ker 
 est un sous groupe normal de G
est un sous groupe normal de G .
.
Démonstration Je ne vous en ferais pas l'affront.



suivant: Structure de l'ensemble quotient
monter: Groupes quotients
précédent: Introduction
Emmanuel_Vieillard-Baron_pour_les.mathematiques
![]() . Alors l'ordre de g
. Alors l'ordre de g ![]() divise l'ordre de G
divise l'ordre de G![]() .
.
![]() . Alors
. Alors
![]() est un sous groupe de G
est un sous groupe de G![]() . Cette affirmation est triviale à vérifier. De plus, par définition de l'ordre d'un élément dans un groupe
. Cette affirmation est triviale à vérifier. De plus, par définition de l'ordre d'un élément dans un groupe![]() , ce sous groupe est de cardinal n. Par application du théorème de Lagrange
, ce sous groupe est de cardinal n. Par application du théorème de Lagrange![]() , n est un diviseur du cardinal de G.
, n est un diviseur du cardinal de G.
![]() alors existe-t-il un élément d'ordre p
alors existe-t-il un élément d'ordre p ![]() dans G ou encore: existe-t-il un sous groupe d'ordre p dans G. La réponse sera donnée par le théorème de Cauchy
dans G ou encore: existe-t-il un sous groupe d'ordre p dans G. La réponse sera donnée par le théorème de Cauchy ![]() pour les éléments d'ordre p et sous certaines conditions sur p, et par le théorème de Sylows
pour les éléments d'ordre p et sous certaines conditions sur p, et par le théorème de Sylows![]() , pour les sous groupes d'ordre p, sous certaines conditions sur p et sur G.
, pour les sous groupes d'ordre p, sous certaines conditions sur p et sur G.
![]() et les classes à droite
et les classes à droite![]() . Nous allons nous
pencher sur cette question dans la fin de ce paragraphe.
. Nous allons nous
pencher sur cette question dans la fin de ce paragraphe.
![]() . On
note
. On
note
![]() le fait que H soit normal dans G.
le fait que H soit normal dans G.
![]() =h'
=h'![]() . Ceci prouve que
. Ceci prouve que
![]() .
.
![]() . Alors pour tout g dans G et tout h dans H, g.h.g
. Alors pour tout g dans G et tout h dans H, g.h.g![]() est élément de H. Donc pour tout g dans
G et tout h dans H, g.h est dans H.g. On a ainsi montré que pour tout élément g de G, gH
est élément de H. Donc pour tout g dans
G et tout h dans H, g.h est dans H.g. On a ainsi montré que pour tout élément g de G, gH![]() Hg. Comme les cardinaux de gH et Hg sont égaux à
celui de H, ils sont égaux entre eux et on a alors bien gH=Hg.
Hg. Comme les cardinaux de gH et Hg sont égaux à
celui de H, ils sont égaux entre eux et on a alors bien gH=Hg.
![]() est un homomorphisme de groupe
est un homomorphisme de groupe ![]() alors le noyau de
alors le noyau de ![]() : Ker
: Ker ![]()
![]() est un sous groupe normal de G
est un sous groupe normal de G![]() .
.