


suivant: Ensemble quotient
monter: Relations d'équivalence
précédent: Introduction
Définition On considère une relation 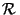 sur un ensemble X. On dira que est une relation d'équivalence si pour tout x,y et z de X elle vérifie:
sur un ensemble X. On dira que est une relation d'équivalence si pour tout x,y et z de X elle vérifie:
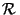 est réflexive: x
est réflexive: x 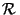 x.
x.
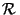 est symétrique: x
est symétrique: x 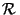 y
y
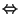 y
y 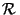 x.
x.
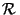 est transitive: si x
est transitive: si x 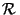 y et que y
y et que y 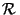 z alors x
z alors x 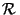 z.
z.
Exemple "être égal à" est une relation d'équivalence (sur n'importe quel ensemble X).
Exemple Sur IN, on considère la relation x 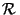 y
y
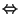 x-y est pair où x et y désignent des éléments quelconques de IN.
x-y est pair où x et y désignent des éléments quelconques de IN. 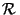 ainsi définie
est une relation d'équivalence (le vérifier!!).
ainsi définie
est une relation d'équivalence (le vérifier!!).
Définition Soit X un ensemble muni d'une relation d'équivalence 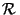 . Soit aussi x un élément de X. On appellera classe d'équivalence de x suivant
. Soit aussi x un élément de X. On appellera classe d'équivalence de x suivant 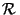 l'ensemble
l'ensemble
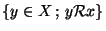 . Un élément y d'une classe d'équivalence sera appelé un représentant de la classe
d'équivalence.
. Un élément y d'une classe d'équivalence sera appelé un représentant de la classe
d'équivalence.
Exemple Pour X=INet avec la relation d'équivalence définie dans l'exemple précédent, la classe d'équivalence de 2 est, comme annoncé dans
l'introduction, l'ensemble des nombres pairs. La classe d'équivalence de 1 est l'ensemble des nombres impairs. Remarquons de plus que ces deux
classes d'équivalence partitionnent IN.
Proposition Une classe d'équivalence n'est jamais vide (!!).
Proposition Si des éléments x et y de X sont dans une même classe d'équivalence alors leurs classes d'équivalences sont identiques.
Exemple Dans l'exemple précédent, la relation d'équivalence choisie nous fournie exactement deux classes d'équivalence sur IN. Tout élément de INa sa
classe d'équivalence égale à une de ces deux là.
Proposition fondamentale L'ensemble des classes d'équivalence d'un ensemble X pour une relation d'équivalence donnée 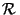 définie une partition de
X.
définie une partition de
X.
Démonstration D'une part, tout élément de X est élément d'une classe d'équivalence de la relation 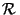 . Au pire, cet élément constitue à lui seul une classe
d'équivalence. D'autre part, si deux classes d'équivalence s'intersectaient en un ensemble non vide, alors de part la transitivité
. Au pire, cet élément constitue à lui seul une classe
d'équivalence. D'autre part, si deux classes d'équivalence s'intersectaient en un ensemble non vide, alors de part la transitivité  de la relation
d'équivalence
de la relation
d'équivalence 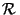 , ceci impliquerait qu'elles seraient en fait égales. L'ensemble des classes d'équivalence d'une relation
, ceci impliquerait qu'elles seraient en fait égales. L'ensemble des classes d'équivalence d'une relation 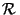 sur X définit ainsi
bien une partition de X.
sur X définit ainsi
bien une partition de X.



suivant: Ensemble quotient
monter: Relations d'équivalence
précédent: Introduction
Emmanuel_Vieillard-Baron_pour_les.mathematiques