


suivant: Application continue sur un
monter: Espaces topologiques connexes
précédent: Introduction
Dans tout ce chapitre (X,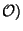 et (Y,
et (Y,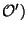 désignent des espaces topologiques.
désignent des espaces topologiques.
Proposition On dira que l'espace topologique (X,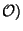 est connexe s'il vérifie l'une des conditions équivalentes suivantes.
est connexe s'il vérifie l'une des conditions équivalentes suivantes.
- Si X est réunion de deux ouverts disjoints alors l'un de ces deux ouverts est vide et l'autre égale à X.
- Si X est réunion de deux fermés disjoints alors l'un de ces deux fermés est vide et l'autre égale à X.
- Si l'on considère
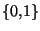 muni de la topologie discrète
muni de la topologie discrète  et
et
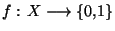 une application continue, alors
une application continue, alors 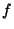 est constante sur X.
est constante sur X.
- Les seuls ensembles à la fois ouverts et fermés de X sont X lui même et l'ensemble vide.
Démonstration
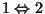 est évident par passage au complémentaire
est évident par passage au complémentaire  .
.
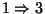 : Soit
: Soit 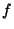 un application continue de X dans
un application continue de X dans
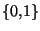 . Alors
. Alors
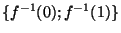 représente une partition de E en deux ouverts (ou deux fermés) de E
représente une partition de E en deux ouverts (ou deux fermés) de E  . Par conséquent, l'un de ces deux ouverts est vide et l'autre égale à X tout entier, ce qui implique bien que
. Par conséquent, l'un de ces deux ouverts est vide et l'autre égale à X tout entier, ce qui implique bien que 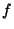 est constante sur X.
est constante sur X.
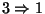 : Soient
: Soient 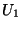 et
et 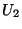 deux ouverts de X qui définissent une partition de X. Soit aussi
deux ouverts de X qui définissent une partition de X. Soit aussi
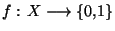 définie par
définie par
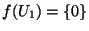 et
et
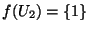 .
. 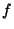 est continue
est continue  et donc constante sur X. Donc l'un des deux ouverts est vide et l'autre égale à X tout entier.Cqfd
et donc constante sur X. Donc l'un des deux ouverts est vide et l'autre égale à X tout entier.Cqfd
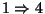 : Soit U un sous ensemble à la fois ouvert et fermé de X. Alors U
: Soit U un sous ensemble à la fois ouvert et fermé de X. Alors U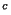 est, lui aussi, un sous ensemble ouvert et fermé de X. Mais U et U
est, lui aussi, un sous ensemble ouvert et fermé de X. Mais U et U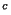 définissent une partition de X en deux ouverts. X étant connexe U est ou vide ou égale à X tout entier.
définissent une partition de X en deux ouverts. X étant connexe U est ou vide ou égale à X tout entier.
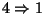 : Supposons que U et V définissent une partition ouverte de X. Le complémentaire de U est alors égale à V et réciproquement V
: Supposons que U et V définissent une partition ouverte de X. Le complémentaire de U est alors égale à V et réciproquement V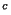 =U. U étant ouvert , V est alors fermé
=U. U étant ouvert , V est alors fermé  . De même U est aussi fermé. Mais X ne possède pas de sous ensemble à la fois ouvert et fermé autre que l'ensemble vide et X. Donc l'un des deux, U ou V est vide l'autre égale à X, ce qui nous donne le premier point.
. De même U est aussi fermé. Mais X ne possède pas de sous ensemble à la fois ouvert et fermé autre que l'ensemble vide et X. Donc l'un des deux, U ou V est vide l'autre égale à X, ce qui nous donne le premier point.
Définition On dira qu'un sous ensemble U de X est un sous espace connexe de X ( ou un connexe de X ) si U est connexe pour la topologie induite de celle de X.
Exemple Un intervalle de IRest connexe dans IR(muni de sa topologie canonique). Les seuls sous ensembles connexes de IRsont d'ailleurs les intervalles



suivant: Application continue sur un
monter: Espaces topologiques connexes
précédent: Introduction
Emmanuel_Vieillard-Baron_pour_les.mathematiques