


suivant: Quelques critères de connexité
monter: Espaces topologiques connexes
précédent: Espaces topologiques connexes
Théorème L'image d'un connexe par une application continue est un sous ensemble connexe de l'espace image de cette application.
Démonstration On supposose ici que (X,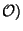 est un espace topologique connexe et soit
est un espace topologique connexe et soit
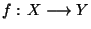 une application continue de X dans Y. Montrons que
une application continue de X dans Y. Montrons que 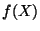 est un connexe de Y. Supposons donc qu'il existe une partition
est un connexe de Y. Supposons donc qu'il existe une partition
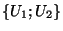 de
de 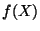 en deux ouverts. Posons
en deux ouverts. Posons
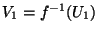 et
et
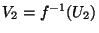 . Les deux ouverts
. Les deux ouverts 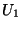 et
et 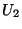 sont des éléments de la topologie induite
sont des éléments de la topologie induite  sur
sur 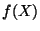 et sont donc de la forme
et sont donc de la forme
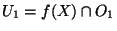 et
et
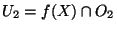 où
où 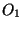 et
et 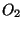 sont des ouverts de Y. De plus, pour i=1,2,
sont des ouverts de Y. De plus, pour i=1,2,
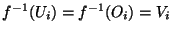 . Comme
. Comme 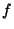 est continue
est continue  , on en déduit que les sous ensembles
, on en déduit que les sous ensembles 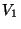 et
et 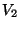 sont des sous ensembles ouverts dans X. De plus, par construction, leur réunion recouvre X et leur intersection est vide.
sont des sous ensembles ouverts dans X. De plus, par construction, leur réunion recouvre X et leur intersection est vide.
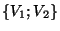 est donc une partition de X en deux ouverts. Comme X est connexe, l'un de ces deux ouverts est vide et l'autre égale à X tout entier. Mais ceci implique que l'image par
est donc une partition de X en deux ouverts. Comme X est connexe, l'un de ces deux ouverts est vide et l'autre égale à X tout entier. Mais ceci implique que l'image par 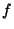 de chacun de ces deux ouverts est, respectivement vide et égale à
de chacun de ces deux ouverts est, respectivement vide et égale à 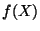 tout entier et donc que l'un des nos deux sous ensembles
tout entier et donc que l'un des nos deux sous ensembles 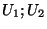 de
de 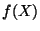 est vide et l'autre égale à
est vide et l'autre égale à 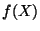 .
. 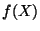 est alors bien connexe.
est alors bien connexe.
Et en application de ce théorème:
Théorème Théo. des valeurs intermédiaires Si une application 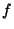 est définie et continue sur un intervalle ]a,b[ de IR(où a et b sont des rééls quelconques pouvant être égales à respectivement
est définie et continue sur un intervalle ]a,b[ de IR(où a et b sont des rééls quelconques pouvant être égales à respectivement 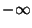 et
et 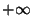 ) , et si de plus a' et b' sont des éléments de ]a,b[ tel que a'<b' alors pour tout
) , et si de plus a' et b' sont des éléments de ]a,b[ tel que a'<b' alors pour tout
![$C\in [f(a'),f(b')]$](/a/t/o/img34.gif) , il existe
, il existe ![$c\in[a',b']$](/a/t/o/img35.gif) tel que
tel que 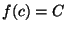 .
.
Démonstration L'image d'un connexe par une application continue est connexe. Or, les intervalles de IRsont les sous ensembles connexes de IR. On en déduit donc que l'image de [a',b'] par f est un intervalle de IR. Tout élément de ce dernier possèdant un antécédent dans [a',b'], Le théorème est démontré.



suivant: Quelques critères de connexité
monter: Espaces topologiques connexes
précédent: Espaces topologiques connexes
Emmanuel_Vieillard-Baron_pour_les.mathematiques