


suivant: Espaces topologiques connexes
monter: Espaces topologiques connexes
précédent: Espaces topologiques connexes
Tout comme les espaces compacts représentaient une généralisation de la notion d'ensembles fermés et bornés dans des espaces non métriques, les espaces connexes seront une généralisation de la notion d'"ensemble d'un seul tenant" (comme, par exemple, les boules de IR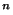 ). Ceci nous permettra de formuler un théorème des valeurs intermédiaire généralisé.
). Ceci nous permettra de formuler un théorème des valeurs intermédiaire généralisé.
La place des espaces connexes est fondamental en analyse car, une propriété topologique (ou analytique) vérifiée localement par un objet sur des espaces de ce type le sera sur l'espace tout entier. Les espaces connexes permettent de transformer une propriété locale en une propriété globale. Cette outil sera souvent utilisé par la suite et dans des leçons aussi diverses que celles touchants au calcul différentiel que celles concernants les fonctions holomorphes (et autre...).
Emmanuel_Vieillard-Baron_pour_les.mathematiques