suivant: Application continue monter: Espaces Topologiques précédent: Suite dans un espace

Espaces topologiques à base dénombrable de voisinage

Proposition Soit F un fermé de (X, $\cal{O}$ ). Soit $(x_n)_{\scriptsize {n \in I\!N\,}}$ , une suite d'éléments de F qui converge vers un élément x de X. Alors x est élément de F.
Démonstration Par définition de la convergence d'une suite, tout voisinage V de x rencontre F en un point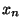

(où n est choisis comme il faut). D'après la définition d'un point adhérent à un ensemble,x est donc point adhérent à F. Mais comme F est fermé, l'ensemble des points adhérents à F se confond avec F

.
Le but de ce paragraphe est de travailler sur la réciproque de cette propriété.
Définition On dit qu'un espace topologique (X, $\cal{O}$ )possède une base dénombrable de voisinage si pour tout x de X, on a:
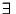
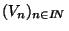
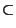
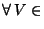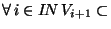$\exists \,$ $(V_n)_{\scriptsize {n \in I\!N\,}}$ $\subset$ $\cal{V}\,$ (x) / $\forall \, V \in$ V $(x) \,\exists\, n \in$ IN $V_n \subset V$ et $\forall \,i\in I\!N\,V_{i+1}\subset$ V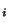

.
Théorème Soit (X, $\cal{O}$ )possédant une base dénombrable de voisinage et soit U un sous ensemble de X. On a équivalence entre:

x est une valeur d'adhérence de U.
Il existe une suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ d'éléments de U convergeant vers x.

$\,$
Démonstration Occupons nous du sens direct: Supposons que x est valeur d'adhérence de U. Alors tout voisinages V de x rencontre U

. En particulier, comme (X, $\cal{O}$ )est à base dénombrable de voisinages, pour tout n dans IN, il existe un voisinage de x: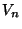

et ce voisinage rencontre U. Choisissons alors, pour n donné dans IN,

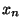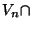dans $V_n \cap$ U. On construit ainsi une suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ . Enfin, pour montrer que cette suite converge vers x, il suffit de remarquer que si V est élément de $\cal{V}\,$ (x) alors il existe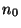

dans INtel 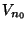$V_{n_0}$ est inclus dans V, et donc 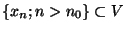$\lbrace x_n;n>n_0 \rbrace \subset V$ , ce qui nous prouve la convergence souhaitée

.
Pour la réciproque, on choisit une suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ convergeant vers x. Pour tout V de $\cal{V}\,$ (x), il existe n dans INtel que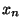

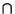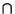est élément de V $\cap$ U. Ainsi pour tout V de $\cal{V}\,$ (x), V $\cap$ U est non vide. Ceci nous assure du fait que x est bien valeur d'adhérence de $(x_n)_{\scriptsize {n \in I\!N\,}}$

.
Voici maintenant un corollaire fondamentale car il donne un critère très pratique pour vérifier qu'un sous ensemble de X est fermé.
Corollaire Soit (X, $\cal{O}$ )un espace topologique à base dénombrable de voisinage et F un sous ensemble de X. On a équivalence entre:

F est fermé.
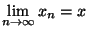Pour toute suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ convergente d'éléments de F ,on a $\displaystyle{\lim_{n\rightarrow \infty}x_n=x}$ est élément de F.

$\,$
Démonstration Supposons que F est fermé. Alors tout point x de F est point adhérent à F

. Donc, d'après la propriété précédente, on peut trouver une suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ d'éléments de F ayant x pour limite.
Réciproquement, supposons que toute suite convergente $(x_n)_{\scriptsize {n \in I\!N\,}}$ d'éléments de F ait sa limite dans F. Prenons un point x de l'adhérence de F. Comme x est un point adhérent à F, on peut construire une suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ d'éléments de F qui converge vers x

. Mais ceci implique, par hypothèse, que x est élément de F et donc que l'adhérence de F est incluse dans F. Ceci équivaut évidemment au fait que F est fermé

suivant: Application continue monter: Espaces Topologiques précédent: Suite dans un espace

Emmanuel_Vieillard-Baron_pour_les.mathematiques