suivant: Espaces topologiques à base monter: Espaces Topologiques précédent: Valeur d'adhérence et adhérence

Suite dans un espace topologique

On considère dans ce paragraphe une suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ de X.
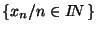Définition On appelle valeur d'adhérence de la suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ tout point adhérent à $\lbrace x_n / n \in I\!N\,\rbrace$ .
Exemple Un élément de la suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ est un point adhérent à $(x_n)_{\scriptsize {n \in I\!N\,}}$ .
Définition On appelle point d' accumulation de la suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ toute valeur d' adhérence de cette suite qui n' est pas élément de la suite.
Définition On dira que $(x_n)_{\scriptsize {n \in I\!N\,}}$ est convergente vers le point x de X si :

$\begin{displaymath}\forall V\in V(x)\, \exists N(V) \in I\!N\,\,;\, \lbrace x_n ; n > N(V) \rbrace \subset V.\end{displaymath}$

Le point x sera appelé la limite de la suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ dans X et on notera:

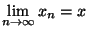
$\displaystyle{\lim_{n\rightarrow \infty}x_n=x}$ .

Remarque Si x est limite de la suite $(x_n)_{\scriptsize {n \in I\!N\,}}$ alors x est valeur d'adhérence de cette suite.
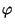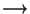Définition Soit $\varphi$ :IN $\longrightarrow$ IN une application strictement croissante. La suite définie par 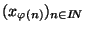$(x_{\varphi(n)})_{\scriptsize {n \in I\!N\,}}$ est appelée sous suite (ou suite extraite) de $(x_n)_{\scriptsize {n \in I\!N\,}}$ .
Remarque Soit 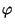$\varphi$ l'aplication définie précédemment. On a l'inclusion:

$\begin{displaymath}\lbrace x_{\varphi(n)}; n\in I\!N\,\rbrace \subset \lbrace x_n; n\in I\!N\,\rbrace.\end{displaymath}$

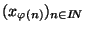Ce qui justifie le nom donné à la suite $(x_{\varphi(n)})_{\scriptsize {n \in I\!N\,}}$ .

suivant: Espaces topologiques à base monter: Espaces Topologiques précédent: Valeur d'adhérence et adhérence

Emmanuel_Vieillard-Baron_pour_les.mathematiques