


suivant: Homéomorphismes
monter: Espaces Topologiques
précédent: Espaces topologiques à base
Soient (X, ) et (Y,
) et (Y, ) deux espaces topologiques.
) deux espaces topologiques.
Définition
On dira qu'une fonction  :X
:X
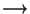 Y est continue en
Y est continue en 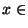 X si
X si
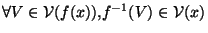
Définition
Une application  :X
:X
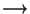 Y sera dite continue sur X si pour tout O de
Y sera dite continue sur X si pour tout O de  ,
, 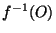 est élément de
est élément de  .
.
Remarque Voir la définition d'une fonction continue dans un espace métrique ( et
et  ) ainsi que la définition d'une fonction mesurable en théorie de la mesure.
) ainsi que la définition d'une fonction mesurable en théorie de la mesure.
La proposition suivante nous assure de la cohérence entre la définition de la continuité en un point et la définition de la continuité sur un espace tout entier (Une fonction est continue sur un espace si et seulement si elle est continue en chaque point de cet espace):
Proposition
Soit  :X
:X
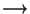 Y On a la série d'équivalence:
Y On a la série d'équivalence:
 est continue sur X.
est continue sur X.
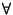 F fermé de Y,
F fermé de Y,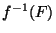 est un fermé de X.
est un fermé de X.
-
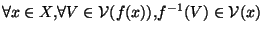

Démonstration
1
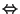 2:On sait que pour tout ensemble A,
2:On sait que pour tout ensemble A,
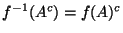 . L'équivalence s'en déduit aussi tôt.
. L'équivalence s'en déduit aussi tôt.
1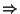 3 Soit x un point de x et y=
3 Soit x un point de x et y= (x). Soit V un élément de
(x). Soit V un élément de  (
( (x)). Nous devons prouver que
(x)). Nous devons prouver que 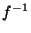 (V) est un voisinage de x. Comme V est un voisinage de
(V) est un voisinage de x. Comme V est un voisinage de  (x), il contient un ouvert O de Y, cet ouvert contenant y.
(x), il contient un ouvert O de Y, cet ouvert contenant y. 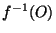 est donc, puisque
est donc, puisque  est continue, un ouvert de X contenant x. Mais cet ouvert est contenu dans
est continue, un ouvert de X contenant x. Mais cet ouvert est contenu dans 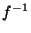 (V). Ce dernier est donc bien un voisinage de x
(V). Ce dernier est donc bien un voisinage de x .
.
3 1 Soit O un ouvert de Y. Montrons que
1 Soit O un ouvert de Y. Montrons que 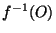 est un ouvert de X. Soit x un élément de
est un ouvert de X. Soit x un élément de 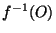 . Comme O est ouvert, on peut trouver un élément V de
. Comme O est ouvert, on peut trouver un élément V de  (
( (x)) tel que V soit inclus dans O
(x)) tel que V soit inclus dans O . Mais
. Mais 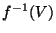 est alors un élément de
est alors un élément de  (x) inclus dans
(x) inclus dans 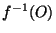 .Cqfd.
.Cqfd.
Théorème
Soient  :X
:X
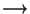 Y et
Y et 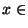 X. Si
X. Si  est continue en x alors
est continue en x alors 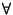
 convergeantes vers x,
convergeantes vers x,
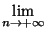 f(
f(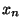 )=f(x).
)=f(x).
Démonstration
Supposons que  est continue en x. Alors pour tout voisinage V de
est continue en x. Alors pour tout voisinage V de  (x),
(x), 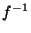 (V) est un voisinage de x. Soit
(V) est un voisinage de x. Soit
 une suite convergeant vers x et soit V un voisinage de
une suite convergeant vers x et soit V un voisinage de  (x). Par définition de la convergence d'une suite
(x). Par définition de la convergence d'une suite  , il existe
, il existe 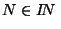 tel que si
tel que si 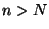 alors x
alors x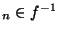 (V) Donc, si n>N alors
(V) Donc, si n>N alors 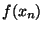 est élément de V. Ceci prouve que
est élément de V. Ceci prouve que
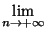 f(
f(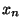 )=
)= (x).
(x).
La réciproque de cette propriété est vraie si l'espace est à base dénombrable de voisinage:
Théorème
Si (X, ) est à base dénombrable de voisinages et si
) est à base dénombrable de voisinages et si
 est une suite convergeant vers x, on a équivalence entre:
est une suite convergeant vers x, on a équivalence entre:
 est continue en x.
est continue en x.
- Pour toute suite
 convergeant vers x,
convergeant vers x,
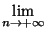 f(
f(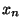 )=f(x).
)=f(x).

Démonstration
Supposons que  n'est pas continue en x. Ceci implique qu'il existe un voisinage V de
n'est pas continue en x. Ceci implique qu'il existe un voisinage V de  (x) tel que
(x) tel que 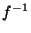 (V) n'est pas un voisinage de x
(V) n'est pas un voisinage de x . Donc U=
. Donc U=
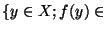 V
V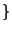 ne contient pas d'ouvert contenant x. Autrement dit, prenant un système fondamentale de voisinage au point x :
ne contient pas d'ouvert contenant x. Autrement dit, prenant un système fondamentale de voisinage au point x :
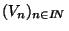 , pour tout n dans IN, on peut trouver un élément
, pour tout n dans IN, on peut trouver un élément 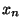 de
de 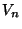 tel que
tel que
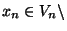 U. La suite
U. La suite 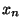 ainsi construite converge vers x
ainsi construite converge vers x  mais la suite
mais la suite
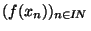 ne rencontre, par construction, jamais V et donc ne converge pas vers
ne rencontre, par construction, jamais V et donc ne converge pas vers 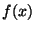 . Cqfd.
. Cqfd.
Définition
Soit  :X
:X
 Y. On dira que
Y. On dira que  est une application ouverte si l'image par
est une application ouverte si l'image par  de tout ouvert de X est un ouvert de Y.
de tout ouvert de X est un ouvert de Y.
Proposition
Si  est bijective, on a équivalence entre:
est bijective, on a équivalence entre:
 est une application ouverte.
est une application ouverte.
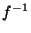 est continue comme application de Y dans X.
est continue comme application de Y dans X.
Démonstration C'est évident!.
Nous considérerons, pour la dernière propriété de ce paragraphe, un troisième espace topologique (Z,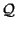 ).
).
Proposition
(Continuité de la composée de deux applications continues) Si  :X
:X
 Y est continue sur X et que
Y est continue sur X et que 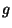 :Y
:Y
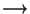 Z est continue sur Y alors
Z est continue sur Y alors 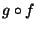 :X
:X
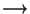 Z est continue sur X.
Z est continue sur X.
Démonstration Soit O un ouvert de Z. Comme 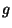 est continue,
est continue, 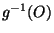 est un ouvert de Y. Mais comme f est continue
est un ouvert de Y. Mais comme f est continue  ,
,
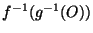 est un ouvert de X. Ce qui prouve que, pour O ouvert quelconque de Z,
est un ouvert de X. Ce qui prouve que, pour O ouvert quelconque de Z,
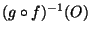 est un ouvert de X, et que
est un ouvert de X, et que 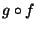 est continue sur X.
est continue sur X.



suivant: Homéomorphismes
monter: Espaces Topologiques
précédent: Espaces topologiques à base
Emmanuel_Vieillard-Baron_pour_les.mathematiques