suivant: Suite dans un espace monter: Espaces Topologiques précédent: Sous ensemble fermé

Valeur d'adhérence et adhérence d'un sous ensemble de X

Définition Soit U une partie de X.On appelera adhérence de U le plus petit fermé de X contenant U. On notera

$\begin{displaymath}\overline{U}\end{displaymath}$

l'adhérence de U.
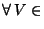
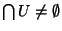
Définition On dira qu'un élément x de X est adhérent au sous ensemble U de X si: $\forall \, V \in$ $\cal{V}\,$ (x), V $\bigcap U \neq \emptyset$
Remarque Tout élément d'un ensemble donné est valeur d'adhérence de cet ensemble.
Proposition L'adhérence d'un sous ensemble de X est égale à l'ensemble de toutes les valeurs d'adhérence de cet ensemble.
Démonstration Soit U un sous ensemble de X et notons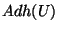

l'ensemble des valeurs d'adhérences de U.
Montrons tout d'abord que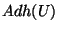

est fermé. Soit x un élément de

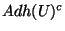. Alors on peut trouver un voisinage V de x tel que ce voisinage n'intersecte pas

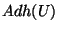. Ce voisinage est donc dans

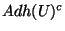. x possède alors un voisinage tout entier dans

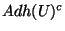. Cela étant vrai pour tout élément x de

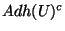on en déduit que

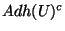est ouvert et donc

que

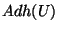est fermé. De plus, d'après la remarque précédente, U est tout entier dans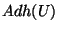

. Donc,

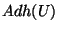est un fermé qui contient U. On peut alors affirmer que l'adhérence de U est une partie de

.
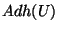Montrons maintenant que si F est un fermé de X contenant U alors F contient nécessairement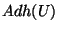

. Soit donc F un fermé de X contenant U et soit x un élément de

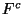. Comme

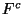est ouvert

, on peut trouver un voisinage V de x inclus dans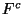

.Ce voisinage et F sont donc disjoints. Il en est donc de même pour ce voisinage et

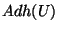. Donc x est élément de

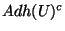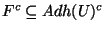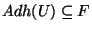. On a alors montré que $F^c \subseteq Adh(U)^c$ et donc que $Adh(U) \subseteq F$ .
Concluons: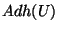

est un fermé contenant U et tout fermé contenant U contient

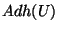. Ce dernier est donc le plus petit fermé contenant U et est donc égale à l'adhérence de U.
Définition On dit que le sous ensemble U de X est dense dans X si

$\begin{displaymath}\overline {U}=X\end{displaymath}$

ou, ce qui est équivalent, si l'intérieur de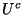

est vide.
Exemple IQest dense dans IR.

suivant: Suite dans un espace monter: Espaces Topologiques précédent: Sous ensemble fermé

Emmanuel_Vieillard-Baron_pour_les.mathematiques