suivant: Intérieur d'un sous ensemble monter: Espaces Topologiques précédent: Topologie sur un ensemble

Topologie induite et engendrée

On considère ici une partie A de X.
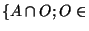
Proposition l'ensemble $\lbrace A\cap O ; O\in$ $\cal{O}\,$ $\rbrace$ definit une topologie sur A que l'on appelle topologie induite de (X, $\cal{O}$ ) sur A.
Démonstration C'est trivial, il suffit de vérifier les trois axiomes définissants une topologie

.
Remarque Si A est ouvert alors les ouverts de la topologie induite de celle de X sur A et les ouverts de X coincident.
Définition Soit $\cal{P}$ une partie de $\cal{P}$ (X). La topologie la moins fine contenant $\cal{P}$ est appelée topologie engendrée par la famille $\cal{P}$ .
Remarque Cette topologie existe toujours. Au pire, c'est la topologie discrète (pour laquelle chaque point est un ensemble ouvert). Chaque élément de $\cal{P}$ est alors bel et bien ouvert (comme réunion quelconque d'ouvert de X).
Exemple

La notion de topologie induite permet en particulier de définir la topologie d'un espace métrique (X,d): C'est la topologie engendrée par les boules ouvertes de cette métrique.
Cette notion permet aussi de définir la topologie produit d'un produit d'espace métrique. C'est la topologie engendrée sur le produit par les produits de boules incluses dans les espaces composants le produit.

suivant: Intérieur d'un sous ensemble monter: Espaces Topologiques précédent: Topologie sur un ensemble

Emmanuel_Vieillard-Baron_pour_les.mathematiques