


suivant: Topologie induite et engendrée
monter: Espaces Topologiques
précédent: Introduction
Dans toute la suite, X désignera un ensemble et  une partie de
une partie de  (X).
(X).
Définition
On dit que (X, )est un espace topologique si
)est un espace topologique si  vérifie:
vérifie:
- X,

 .
.
- Une intersection finie d'éléments de
 est encore élément de
est encore élément de  .
.
- Une réunion quelconque d'éléments de
 est encore élément de
est encore élément de  .
.
Un élément de  sera appelé un sous ensemble ouvert de X. ( On utilisera le plus souvent le mot ouvert à la place de sous ensemble ouvert).
Se donner
sera appelé un sous ensemble ouvert de X. ( On utilisera le plus souvent le mot ouvert à la place de sous ensemble ouvert).
Se donner  sur X vérifiant les 3 axiomes précédents revient à se donner une topologie sur X.
sur X vérifiant les 3 axiomes précédents revient à se donner une topologie sur X.
Définition
On appelle topologie discrète sur un ensemble X la topologie sur X pour laquelle tout sous ensemble de X est ouvert. (En particulier, tout point de X définit un sous ensemble ouvert de X). Cette topologie est égale à  (X).
(X).
Définition
On appelle topologie grossière sur un ensemble X la topologie  donnée par
donnée par  =
=
 .
.
On considère désormais un espace topologique (X, ).
).
Définition
Soit V 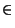
 (X)et x
(X)et x 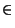 X.
On dira que V est un voisinage de x si il existe un ouvert U de X tel que x soit élément de U et U soit inclus dans V.
X.
On dira que V est un voisinage de x si il existe un ouvert U de X tel que x soit élément de U et U soit inclus dans V.
On notera  (x) l'ensemble de tous les voisinages de x.
(x) l'ensemble de tous les voisinages de x.
Remarque Si O 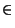
 et si x
et si x 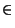 O alors O
O alors O 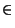
 (x).
(x).
Proposition
Un sous ensemble O de X est ouvert si et seulement si il est voisinage de chacun de ses points.
Démonstration
D'après la remarque précédente, le sens direct est évident. Montrons la réciproque. Supposons donc que O est un ensemble voisinage de chacun de ses points. Pour tout x dans O, on peut alors trouver un sous ensemble O(x) de O tel que O(x) soit ouvert et x élément de O(x). On peut même écrire:
O est donc réunion quelconque d'ouverts. Ceci implique  évidemment que O est ouvert.
évidemment que O est ouvert.
Définition
Soient  et
et  deux topologies sur X. On dira que
deux topologies sur X. On dira que  est plus fine que
est plus fine que  si
si  est incluse dans
est incluse dans  .
.
Remarque ``Etre plus fine que'' est une relation d'ordre (non totale) sur l'ensemble de toutes les topologies de X.



suivant: Topologie induite et engendrée
monter: Espaces Topologiques
précédent: Introduction
Emmanuel_Vieillard-Baron_pour_les.mathematiques