suivant: Topologie sur un ensemble
monter: Espaces Topologiques
précédent: Espaces Topologiques
Le concept de mesure est culturel. Les peuples aborigènes, par exemple, n'en ont pas la connaissance et ont du développer d'autres outils pour localiser les lieux dans l'espace. Ainsi, si l'on se pose le problème de décrire un chemin permettant, partant d'un point A, de rejoindre un point B (comme sur la figure ci contre), on pourrait proposer deux types de réponse:
- la première, qui est celle à laquelle nous sommes habituée: ''Pour aller de A à B, longer le chemin sur 5 km, puis à votre droite, la rivière sur 3 km''
- la seconde, du type aborigène, serait: ''Avancer sur le chemin jusqu'à arriver au voisinage d'un grand arbre, longer alors la rivière sur votre droite et ce jusqu'à approcher à la fois la périphérie de la forêt et celle de la colline.
Il en est des espaces mathématiques comme des cultures humaines. Certains sont en effet étrangers à toute métrique (penser à par exemple
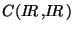, l'espace des fonctions continues de IRdans IR), d'autres aussi échappent suffisamment à notre perception pour qu'aucune métrique naturelle ne s'impose (quelle métrique mettre sur un tore ou sur
![$I\!R\,P[2]=S^2/(x \sim -x)$](/a/t/g/img2.gif)
, l'espace projectif réél de dimension 2 (qui est aussi l'ensemble de toutes les droites vectorielles non orientées de l'espace IR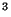
)). Devons nous alors renoncer, pour de tels ensembles, aux notions de convergences (pour lesquelles il est justement nécessaire de définir ce que signifie être près de )? C'est à ce niveau qu'intervient la topologie et son formalisme.
suivant: Topologie sur un ensemble
monter: Espaces Topologiques
précédent: Espaces Topologiques
Emmanuel_Vieillard-Baron_pour_les.mathematiques