


monter: Espaces Topologiques
précédent: Application continue
Soient (X, ) et (Y,
) et (Y, ) deux espaces topologiques.
) deux espaces topologiques.
Définition
On dit que  :X
:X
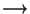 Y est un homéomorphisme si:
Y est un homéomorphisme si:
 est bijective.
est bijective.
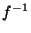 et
et  sont continues.
sont continues.

Définition
On dira que deux espaces sont homéomorphes si l'on peut définir un homéomorphisme entre ces deux espaces.
Ainsi, si l'on peut définir un homéomorphisme entre deux espaces topologiques, au delà d'une correspondance ponctuelle de chacun de ces deux espaces, c'est aussi un corespondance aux niveaux des éléments de leur topologie. Les homéomorphimes jouent en topologie un rôle absolument équivalent à celui des isomorphismes en algèbre. On dira d'ailleurs de deux espaces homéomorphes qu'ils sont topologiquement équivalent. Toute propriété topologique vérifiée par l'un le sera par l'autre. Ainsi, prenant un peu d'avance sur les leçons prochaines, si l'un des espaces est compact (connexe,...), il en sera de même pour l'autre.
L'intérêt d'une telle notion est double. En plus de servir à la classification des espaces topologiques, l'homéomorphie sert à transporter des propriétés topologiques d'un objet vers un autre. Une propriété topologique difficile à prouver pour un espace A sera peut-être plus facile à montrer sur un espace B qui lui est homéomorphe.
Proposition
 :X
:X
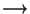 Y est un homéomorphisme si et seulement si
Y est un homéomorphisme si et seulement si  vérifie les trois propriétés suivantes:
vérifie les trois propriétés suivantes:
 est bijective.
est bijective.
 est continue.
est continue.
 est ouverte
est ouverte  .
.

Proposition
``Etre homéomorphe à'' est une relation d'équivalence.



monter: Espaces Topologiques
précédent: Application continue
Emmanuel_Vieillard-Baron_pour_les.mathematiques