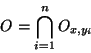suivant: Continuité et compacité monter: Espaces topologiques compacts précédent: Suites dans un espace

Sous espaces compacts

On suppose dorénavant que (X,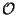 $\cal{O}\,$ ) est un espace séparé.
Définition On dit d'un sous ensemble de (X,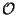 $\cal{O}\,$ ) qu'il est compact s'il est compact pour la topologie induite

de celle de X.
Remarque Afin de simplifier l'utilisation des sous espaces compacts, on donne la caractérisation suivante:
Proposition On a équivalence entre:

K est un sous espace compact de X.
Pour toute famille $(U_i)_{\scriptsize {i \in I}}$ d'ouverts de X tel que

$\begin{displaymath}K \subset \displaystyle{\bigcup_{i \in I} U_i},\end{displaymath}$

il existe I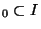 $_0\subset I$ de cardinal fini tel que

$\begin{displaymath}K \subset \displaystyle{\bigcup_{i \in I_0} U_i}.\end{displaymath}$

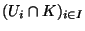Démonstration Si $(U_i)_{\scriptsize {i \in I}}$ est une famille d'ouverts de X, alors $(U_i\cap K)_{\scriptsize {i \in I}}$ est une famille d'ouverts de K pour la topologie induite de X sur K

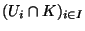. Si K est compact, et que $(U_i\cap K)_{\scriptsize {i \in I}}$ est un recouvrement ouvert de K, on peut en extraire un recouvrement fini et on aura nécessairement

$\begin{displaymath}K \subset \displaystyle{\bigcup_{i \in I_0} U_i}\end{displaymath}$

où I

désigne une sous partie finie de I. Réciproquement, si pour toute famille $(U_i)_{\scriptsize {i \in I}}$ vérifiant

$\begin{displaymath}K \subset \displaystyle{\bigcup_{i _in I} U_i},\end{displaymath}$

on peut extaire une sous famille finie recouvrant K alors cela prouve que pour toute famille d'ouvert de K (pour la topologie induite de X sur K) et recouvrant K, on peut extraire une sous famille finie recouvrant K. K est donc compact pour la topologie induite.

On comprendra la nécessité de supposer qu'un espace compact est un espace séparé en étudiant la proposition suivante.
Théorème Tout compact est fermé.
Démonstration Soit K un compact de X.(On peut avoir K=X).Montrons que K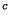

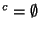est ouvert. Si K $^c=\emptyset$ alors la démonstration est terminée. Sinon soit 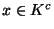$x\in K^c$ . Comme X est un espace séparé, pour tout y dans K, on peut trouver un ouvert 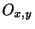$O_{x,y}$ contenant x et un ouvert

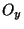contenant y tel que 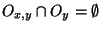$O_{x,y}\cap O_y=\emptyset$ . Mais on a l'inclusion

$\begin{displaymath}K\subset \displaystyle{\bigcup_{y \in K} O_y}.\end{displaymath}$

La famille 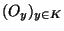$(O_y)_{\scriptsize {y \in K}}$ definit donc un recouvrement ouvert de K. De ce recouvrement, on peut extraire un recouvrement fini 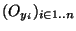$(O_{y_i})_{\scriptsize {i \in 1..n}}$ . Posant

$\begin{displaymath}O=\displaystyle{\bigcap_{i=1}^n O_{x,y_i}}\end{displaymath}$

(qui est ouvert comme intersection finie d'ouverts

), on construit un ouvert de O contenant x et disjoint de K. On montre ainsi bien que K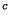

est ouvert et donc que K est fermé

.
Théorème Tout fermé dans un compact est compact.
Démonstration Soient F un fermé et K un compact de X contenant F. Soit aussi $(U_i)_{\scriptsize {i \in I}}$ une famille d'ouverts (ouverts pour la topologie de K) dont la réunion contient K. La famille 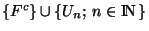$\lbrace F^c \rbrace \cup \lbrace U_n ;\,n\in {\rm I\!N\,}\rbrace$ est un recouvrement ouvert de K. On peut donc en extraire un recouvrement fini de K 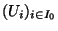$(U_i)_{\scriptsize {i \in I_0}}$ ou I

est une partie finie de I. Mais alors

$\begin{displaymath}F \subset \displaystyle{\bigcup_{i \in I_0} U_i},\end{displaymath}$

et F est compact Cqfd.
Proposition

Une réunion finie de sous espaces compacts est compacte.
Une intersection quelconque de sous espaces compacts est compacte.

$\,$
Démonstration

Soit 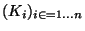$(K_i)_{\scriptsize {i \in =1...n}}$ une famille finie de sous espaces compacts. Soit K la réunion des éléments de cette famille et 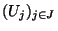$(U_j)_{\scriptsize {j \in J}}$ un recouvrement ouvert de K. Pour tout i=1...n, 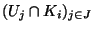$(U_j\cap K_i)_{\scriptsize {j \in J}}$ est donc un recouvrement ouvert de K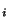. Mais comme chaque K 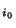$_{i_0}$ est compact, pour tout 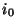=1...n, on peut trouver un sous-ensemble fini J 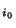$_{i_0}$ de J tel que K 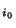$_{i_0}$ soit recouvert par la famille finie d'ouverts 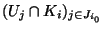$(U_j\cap K_i)_{\scriptsize {j \in J_{i_0}}}$ . Mais la famille 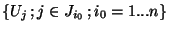$\lbrace U_j \,; j\in J_{i_0}\,;i_0=1...n \rbrace$ est finie, extraite de la famille 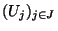$(U_j)_{\scriptsize {j \in J}}$ et recouvre K. D'un recouvrement quelconque de K, on a extrait un recouvrement fini et on a ainsi bien montré que K est compact.
Soit 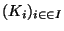$(K_i)_{\scriptsize {i \in \in I}}$ une famille finie de sous espaces compacts. Cette fois ci K désignera l'intersection des éléments de cette famille. Remarquons tout d'abord que K est fermé comme intersection quelconque de fermés . De plus, pour tout i dans I, K est inclus dans K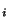. Donc K est un sous ensemble fermé d'un espace compact . C'est donc un espace compact.

$\,$

suivant: Continuité et compacité monter: Espaces topologiques compacts précédent: Suites dans un espace

Emmanuel_Vieillard-Baron_pour_les.mathematiques