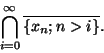suivant: Sous espaces compacts monter: Espaces topologiques compacts précédent: Notions de base

Suites dans un espace compact

Nous allons voir ici une application fondamentale aux espaces métriques du corollaire précédent.
On a vu, dans le cas des espaces métriques, la propriété suivante:
Proposition Si (X,d) est un espace métrique, si 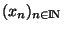$(x_n)_{\scriptsize {n \in {\rm I\!N\,}}}$ est une suite de X et x est un point de X, on a l'équivalence suivante:
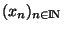$(x_n)_{\scriptsize {n \in {\rm I\!N\,}}}$ admet x comme point d'accumulation

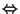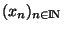
$\Leftrightarrow$ On peut extraire de $(x_n)_{\scriptsize {n \in {\rm I\!N\,}}}$

une sous suite convergeant vers x.
Théorème Toute suite d'un espace métrique compact possède un point d'accumulation.
Démonstration En effet, on a vu dans le cours sur les espaces métriques que l'ensemble des valeurs d'adhérence d'une suite 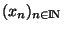$(x_n)_{\scriptsize {n \in {\rm I\!N\,}}}$ est donné par

$\begin{displaymath}\displaystyle{\bigcap_{i=0}^\infty \overline{\lbrace x_n;n>i\rbrace}}.\end{displaymath}$

Posons

$\begin{displaymath}F_i=(\overline{\lbrace x_n;n>i\rbrace})_{i\in {\rm I\!N\,}}.\end{displaymath}$

La famille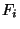

est bien une suite décroissante de fermés non vides. Et donc, par application de la proposition précédente, l'intersection de tous les éléments de cette famille est non vide. L'ensemble des valeurs d'adhérence de la suite 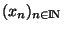$(x_n)_{\scriptsize {n \in {\rm I\!N\,}}}$ est par conséquent non vide.Cqfd.
Remarque On pourrait se poser le problème de la réciproque. Donnons nous (X,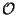 $\cal{O}\,$ ) un espace ayant la propriété : De toutes suites de X, on peut extraire une sous-suite convergente. Peut on alors affirmer que (X, 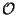$\cal{O}\,$ ) est compact? La réponse, dans le cas métrique, est positive et est donnée par le Théo. de Bolzano-Weierstrass.

suivant: Sous espaces compacts monter: Espaces topologiques compacts précédent: Notions de base

Emmanuel_Vieillard-Baron_pour_les.mathematiques