


monter: Espaces topologiques compacts
précédent: Sous espaces compacts
Théorème fondamental L'image d'un compact par une application continue est compacte.
Démonstration Soient K un compact de (X,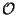 ), (Y,
), (Y,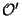 ) un espace topologique et
) un espace topologique et
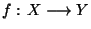 une application continue de X dans Y
une application continue de X dans Y  . Soit
. Soit
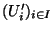 un recouvrement ouvert de
un recouvrement ouvert de 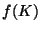 (pour la topologie induite
(pour la topologie induite  sur
sur 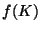 ...). On a donc
...). On a donc
Rappelons que si A et B désignent deux ensembles quelconques de Y alors
Alors
Mais 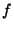 étant continue
étant continue  , chaque
, chaque
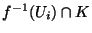 est un ouvert de K (pour la topologie induite
est un ouvert de K (pour la topologie induite  de X sur K).Comme K est compact, on peut extraire de la famille
de X sur K).Comme K est compact, on peut extraire de la famille
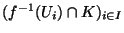 un recouvrement fini de K
un recouvrement fini de K
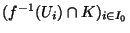 (où I
(où I est une sous partie finie de I). On a alors, comme
est une sous partie finie de I). On a alors, comme
Et donc, du recouvrement initial de 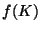 , on a extrait un recouvrement fini, ce qui prouve que
, on a extrait un recouvrement fini, ce qui prouve que 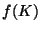 est compact.
est compact.
Remarque Si 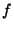 est un homéomorphisme
est un homéomorphisme  de (X,
de (X,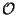 ) dans (Y,
) dans (Y,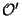 ) et que X est compact, il en est de même de Y.
) et que X est compact, il en est de même de Y.



monter: Espaces topologiques compacts
précédent: Sous espaces compacts
Emmanuel_Vieillard-Baron_pour_les.mathematiques