


suivant: Application continue sur un
monter: Espaces métriques produits
précédent: Notions de base
Théorème Soit
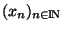 une suite de X.
une suite de X.
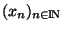 est convergente sur X
est convergente sur X  pour la topologie (métrique) produit si et seulement si ses suites coordonnées sont convergentes pour la topologie de l'espaces auxquels elles appartiennent. De plus, la limite
pour la topologie (métrique) produit si et seulement si ses suites coordonnées sont convergentes pour la topologie de l'espaces auxquels elles appartiennent. De plus, la limite  de la suite
de la suite
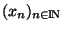 est égale à (
est égale à (
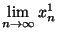 ,...,
,...,
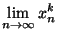 ).
).
Démonstration Soit la suite d'éléments de X
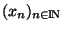 =
=
 où
où
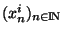 incluse dans
incluse dans 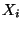 .
.
On sait que si un application f est continue en un point x d'un espace métrique (X,d) vers un espace métrique (Y,d) alors si
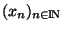 est une suite convergeant vers x, on
est une suite convergeant vers x, on
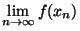 =
=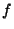 (
(
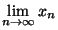 )
)  . D'autre part, les applications
. D'autre part, les applications 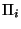 sont continues
sont continues  pour i=1,...,k. Donc
pour i=1,...,k. Donc
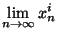 =
=
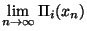 =
=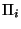 (
(
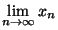 )=
)=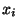
 et les suites
et les suites  sont bien convergentes sur
sont bien convergentes sur 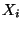
 . De plus, leur limite est
. De plus, leur limite est 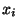 .
.
Montrons maintenant que si les suites coordonnées
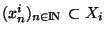 pour i=1,..,k convergent vers
pour i=1,..,k convergent vers 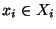 alors la suite
alors la suite
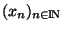 =
=
 converge vers
converge vers
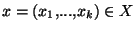
 . Pour ce faire, prenons
. Pour ce faire, prenons 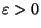 ainsi qu'une boule
ainsi qu'une boule
 =
=
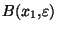
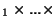
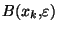
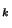 dans X. Pour tout i=1..k, il existe
dans X. Pour tout i=1..k, il existe
 tel que si n>
tel que si n>
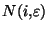 alors
alors 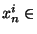
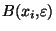
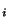 . Prenons
. Prenons
On peut alors affirmer que si n>
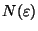 alors
alors 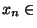
 .
.



suivant: Application continue sur un
monter: Espaces métriques produits
précédent: Notions de base
Emmanuel_Vieillard-Baron_pour_les.mathematiques