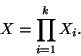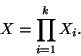suivant: Suites dans un espace
monter: Espaces métriques produits
précédent: Introduction
On considère dans ce chapitre une famille d'espaces métriques
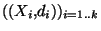
 et soit
et soit
Définition On appelle métrique produit la métrique
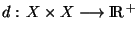 définie par : si
définie par : si
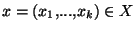 et
et
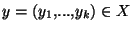 alors
alors
Démonstration On vérifie sans peine que l'application ainsi définie sur X est bien une métrique  .
.
On peut alors énoncer la définition :
Définition L'espace (X,d) est l'espace métrique produit des
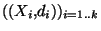 .
.
Proposition Soit r>0 et
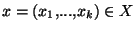 . Soit
. Soit 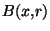 la boule de X de rayon x et de centre r relative à la métrique d
la boule de X de rayon x et de centre r relative à la métrique d  . Notons, pour i=1..k,
. Notons, pour i=1..k, 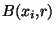
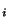 la boule de
la boule de 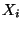 de centre
de centre 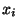 et de rayon r relative à la métrique
et de rayon r relative à la métrique 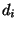
 . Alors
. Alors 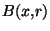 =
=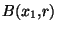
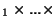
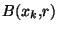
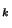 .
.
Démonstration Soit
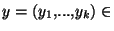
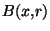 . Alors, pour tout i=1,...,k, on a
. Alors, pour tout i=1,...,k, on a
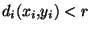 et donc
et donc 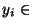
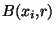
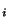
 .
.
Réciproquement, si, pour tout i=1,...,k, 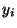 vérifie
vérifie
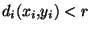 alors
alors 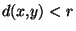 et
et 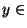
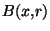 .
.
Définition Pour tout i=1..k, on appelle projecteur de X sur X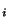 l'application
l'application
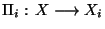 qui à un élément
qui à un élément
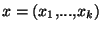 de X associe
de X associe 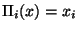 .
.
Proposition Les applications 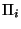 pour i=1,..,k sont 1-Lipschitzienne
pour i=1,..,k sont 1-Lipschitzienne  et sont donc continues
et sont donc continues  .
.
Démonstration C'est immédiat, via la définition des 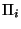 .
.
Proposition Les projecteurs sont des applications ouvertes  .
.
Démonstration Soit i un entier compris entre 1 et k et soit U un ouvert  de (X,d). On veut montrer que
de (X,d). On veut montrer que 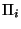 est ouverte, ce qui revient à montrer que
est ouverte, ce qui revient à montrer que 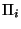 (U) est un ouvert de
(U) est un ouvert de 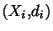
 . Soit x un point de U. Comme U est ouvert, on peut trouver une boule ouverte
. Soit x un point de U. Comme U est ouvert, on peut trouver une boule ouverte 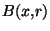
 incluse dans U
incluse dans U  . Mais cette boule est, comme nous l'avons vu, de la forme
. Mais cette boule est, comme nous l'avons vu, de la forme 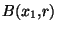
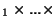
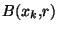
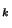
 . Donc
. Donc 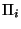 (
( 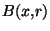 )=
)=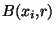
 . Cette dernière boule est donc incluse dans
. Cette dernière boule est donc incluse dans 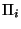 (U), ce qui nous prouve que
(U), ce qui nous prouve que 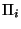 (U) est ouvert
(U) est ouvert  et que
et que 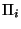 est une application ouverte
est une application ouverte  .
.
Proposition La topologie induite  par la métrique produit est la moins fine
par la métrique produit est la moins fine  pour laquelle les projecteurs sont continues. C'est donc la topologie produit.(Cf les espaces topologiques produits
pour laquelle les projecteurs sont continues. C'est donc la topologie produit.(Cf les espaces topologiques produits ).
).
Démonstration On sait déjà que les projecteurs sont continues pour la métrique produit  . Montrons donc que cette topologie est la moins fine
. Montrons donc que cette topologie est la moins fine  pour laquelle cela fonctionne. Supposons qu'il existe une topologie moins fine,
pour laquelle cela fonctionne. Supposons qu'il existe une topologie moins fine, 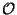 , que celle conséquente à la métrique produit et pour laquelle les projecteurs sont continues. Cela signifie qu'il existe des ouverts de (X,d) qui ne sont pas éléments de
, que celle conséquente à la métrique produit et pour laquelle les projecteurs sont continues. Cela signifie qu'il existe des ouverts de (X,d) qui ne sont pas éléments de  . Comme les projecteurs sont continues, les boules
. Comme les projecteurs sont continues, les boules 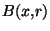 =
=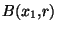
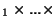
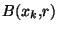
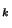 sont des ouverts de
sont des ouverts de 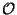
 . Des réunions de telles boules sont donc encore des ouverts de
. Des réunions de telles boules sont donc encore des ouverts de 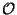
 . Mais tout ouvert de (X,d) est réunion de ces boules. (En effet, par définition d'un ouvert U
. Mais tout ouvert de (X,d) est réunion de ces boules. (En effet, par définition d'un ouvert U  dans un espace métrique, pour tout élément x de U, on peut trouver un réél positif r
dans un espace métrique, pour tout élément x de U, on peut trouver un réél positif r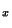 tel que la boule de centre x et de rayon r
tel que la boule de centre x et de rayon r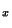 est incluse dans U. En prenant la réunion de toutes ces boules pour chaque x appartenant U, on obtient U.) Donc tout ouvert de (X,d) est ouvert de
est incluse dans U. En prenant la réunion de toutes ces boules pour chaque x appartenant U, on obtient U.) Donc tout ouvert de (X,d) est ouvert de 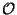
 et la topologie de (X,d) est équivalente à la topologie
et la topologie de (X,d) est équivalente à la topologie 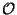 . On a ainsi bien montré que la topologie définie par la métrique produit était équivalente à la topologie produit.
. On a ainsi bien montré que la topologie définie par la métrique produit était équivalente à la topologie produit.



suivant: Suites dans un espace
monter: Espaces métriques produits
précédent: Introduction
Emmanuel_Vieillard-Baron_pour_les.mathematiques