


suivant: Propriétés des espaces métriques
monter: Espaces métriques produits
précédent: Suites dans un espace
On considérera ici, en plus de l'espace métrique produit (X,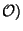 déjà définit précédemment, un espace métrique (Y,d').
déjà définit précédemment, un espace métrique (Y,d').
Proposition L'application
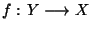 est continue sur Y pour les métriques respectives de X et Y si et seulement si les applications
est continue sur Y pour les métriques respectives de X et Y si et seulement si les applications 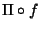 sont continues sur Y pour tout i=1,..,k.
sont continues sur Y pour tout i=1,..,k.
Démonstration Supposons que 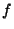 est continue sur Y. Alors comme la composée de deux applications continues est continue
est continue sur Y. Alors comme la composée de deux applications continues est continue  , les applications
, les applications 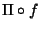 sont continues pour tout i=1,..,k.
sont continues pour tout i=1,..,k.
Supposons maintenant que, pour tout i=1,..,k, 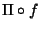 est continue. Pour montrer que
est continue. Pour montrer que 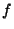 est continue sur Y, il suffit qu'elle soit continue en chaque point x de Y
est continue sur Y, il suffit qu'elle soit continue en chaque point x de Y  . Prenons donc x dans Y et choisissons une suite
. Prenons donc x dans Y et choisissons une suite
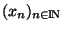 de points de Y convergeant vers x. Montrer que
de points de Y convergeant vers x. Montrer que 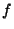 est continue en x revient à montrer l'égalité
est continue en x revient à montrer l'égalité
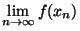 =
=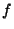 (
(
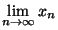 )
)  . Si l'on note, pour tout i=1,...,k,
. Si l'on note, pour tout i=1,...,k,
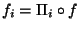 , on a, d'après le théorème précédent sur les suites coordonnées
, on a, d'après le théorème précédent sur les suites coordonnées
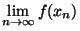 =(
=(
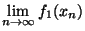 ,...,
,...,
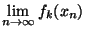 ). Mais comme les applications
). Mais comme les applications 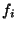 sont continues en x, (
sont continues en x, (
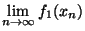
 ,...,
,...,
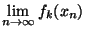 )=
)=
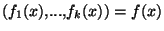 . On a donc bien montré l'égalité voulue et f est bel et bien continue en x
. On a donc bien montré l'égalité voulue et f est bel et bien continue en x
Proposition Soit (X,d) un espace métrique. L'application
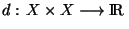 est continue ( et même 2-Lipschitzienne
est continue ( et même 2-Lipschitzienne  ) sur
) sur 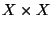 muni de la topologie produit héritée de la métrique d.
muni de la topologie produit héritée de la métrique d.
Démonstration Posons
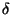 n'est rien d'autre que la métrique produit héritée de d sur
n'est rien d'autre que la métrique produit héritée de d sur 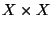 . De plus
. De plus
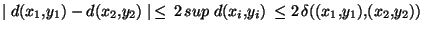 Cqfd.
Cqfd.



suivant: Propriétés des espaces métriques
monter: Espaces métriques produits
précédent: Suites dans un espace
Emmanuel_Vieillard-Baron_pour_les.mathematiques