next up previous
suivant: Le théorème de Baire monter: Espaces métriques complets précédent: Propriétés

Théorème du point fixe

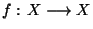Soient (X,d) un espace métrique. On s'intéresse dans cette partie à une application $f: X\longrightarrow X$.
Définition On dit que x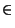$\in$X est un point fixe de 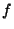$f$ si $f(x)=x$.
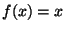Définition Soient (X,d) et (Y,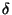$\delta$) deux espaces métriques. Soit k un réél strictement positif. On dit que 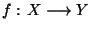$f: X\longrightarrow Y$ est lipschitzienne de rapport k si 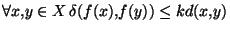$\forall x,y\in X \delta(f(x),f(y))\leq kd(x,y)$. Si de plus k<1, on dit que f est contractante.
Remarque Si 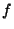$f$ est lipschitzienne, elle est continue .
Théorème (du point fixe) Si (X,d) est complet et que 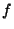$f$ est contractante alors 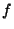$f$ possède un point fixe dans X. De plus, ce point fixe est unique.
Démonstration Soit x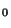$_0$ un élément de X. Posons, pour tout n dans IN, 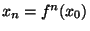$x_n=f^n(x_0)$. On a donc, pour tout n 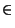$\in$ IN 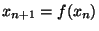$x_{n+1}=f(x_n)$. Supposons que cette suite converge vers un élément x de X. On a alors
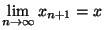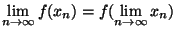$\displaystyle{\lim_{n\rightarrow \infty}x_{n+1}=x}$= $\displaystyle{\lim_{n\rightarrow \infty}f(x_n)=f(\lim_{n \rightarrow \infty}{x_n})}$=f(x)
et donc x est un point fixe de 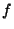$f$.(la troisième égalité provient de la continuité de f ). Il s'agit donc de montrer que cette suite est convergente, ou encore, comme X est complet, qu'elle est de Cauchy.
Mais pour tout m,n dans IN, on a, grâce à l'inégalité triangulaire :

\begin{displaymath}d(x_n,x_{n+m})=d(f^n(x_0),f^{n+m}(x_0)) \leq d(f^n(x_0),f^{n+1}(x_0))+...+d(f^{n+m-1}(x_0),f^{n+m}(x_0))\end{displaymath}

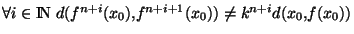Comme f est contractante, $ \forall i \in {\rm I\!N } d(f^{n+i}(x_0),f^{n+i+1}(x_0)) \neq k^{n+i}d(x_0,f(x_0))$.
On a alors

\begin{displaymath}d(x_n,x_{n+m})\leq k^{n}d(x_0,f(x_0))+...k^{n+m-1}d(x_0,f(x_0))=k^n(1+k+...+k^{n+m-1})d(x_0,f(x_0))\end{displaymath}

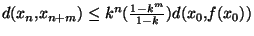
On a alors montré que: $d(x_n,x_{n+m})\leq k^{n} ({\frac{1-k^m}{1-k}})d(x_0,f(x_0))$
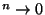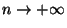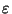Mais comme f est contractante, k<1 et donc k $^n \rightarrow 0$ quand $n \rightarrow +\infty$. Pour $\varepsilon$>0 donné, on peut alors trouver N assez grand tel que si n>N et m>0 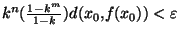$ k^{n} ({\frac{1-k^m}{1-k}})d(x_0,f(x_0))<\varepsilon$ . Ceci prouve que la suite 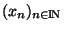$(x_n)_{\scriptsize {n \in {\rm I\!N }}}$ est de Cauchy .
Montrons par l'absurde l'unicité du point fixe. Supposons donc que 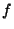$f$ ait deux points fixes x et y. Comme 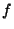$f$ est contractante, on a 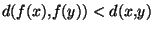$d(f(x),f(y)) < d(x,y) $. Mais comme x et y sont des points fixes 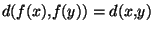$d(f(x),f(y))=d(x,y)$. En comparant ces deux expressions, on aboutit immédiatemment à une contradiction.
Corollaire Si (X,d) est complet et que 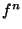$f^n$ est contractante alors 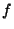$f$ possède un point fixe dans X. De plus, ce point fixe est unique.
Démonstration Comme 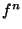$f^n$ est contractante, il existe un élément x de X qui est point fixe de 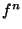$f^n$. Mais alors 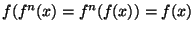$f(f^n(x)=f^n(f(x))=f(x)$. Donc 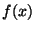$f(x)$ est aussi un point fixe de 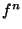$f^n$. Mais d'après le théorème précédent, le point fixe de 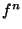$f^n$ est unique. Donc f(x)=x.
next up previous
suivant: Le théorème de Baire monter: Espaces métriques complets précédent: Propriétés
Emmanuel_Vieillard-Baron_pour_les.mathematiques