


suivant: Théorème du point fixe
monter: Espaces métriques complets
précédent: Notions de base
Proposition Tout sous ensemble fermé d'un espace complet est complet.
Démonstration Soit F un fermé de X et soit
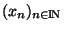 une suite de Cauchy de F. Cette suite est donc convergente dans X. Notons x sa limite. Comme F est un fermé dans un espace métrique, toute suite convergente de points de F a sa limite dans F
une suite de Cauchy de F. Cette suite est donc convergente dans X. Notons x sa limite. Comme F est un fermé dans un espace métrique, toute suite convergente de points de F a sa limite dans F  . Donc x est élément de F.
. Donc x est élément de F.
Proposition Tout sous espace complet d'un espace métrique est fermé.
Démonstration Notons (X,d) l'espace métrique et U la partie de X qui est complète pour la métrique induite  . Pour vérifier, dans un espace métrique, qu'un sous ensemble est fermé, il suffit de vérifier que toute suite convergente de ce sous ensemble a sa limite dans le sous ensemble
. Pour vérifier, dans un espace métrique, qu'un sous ensemble est fermé, il suffit de vérifier que toute suite convergente de ce sous ensemble a sa limite dans le sous ensemble  . Prenons donc une suite convergente
. Prenons donc une suite convergente
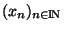 de U. Comme cette suite est convergente, elle est de Cauchy
de U. Comme cette suite est convergente, elle est de Cauchy  . Mais notre sous ensemble U étant complet, sa limite est nécessairement dans U. On montre ainsi que U est fermé.
. Mais notre sous ensemble U étant complet, sa limite est nécessairement dans U. On montre ainsi que U est fermé.
Définition On appelle diamètre d'un élément A de 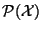 le nombre
le nombre 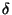 (A)=
(A)=
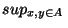 d(x,y).
d(x,y).
Remarque Le diamètre d'une partie de X peut être infinie.
La prop. suivante est parfois utile dans les démonstrations faisant intervenir la complétude.
Proposition On suppose que (X,d) est complet. Soit
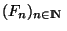 une famille décroissante de fermés de X pour laquelle
une famille décroissante de fermés de X pour laquelle
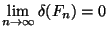 . Il existe alors un unique élément x de X tel que
. Il existe alors un unique élément x de X tel que
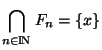 .
.
Démonstration
Soit donc
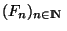 une famille décroissante de fermés dont le diamêtre tend vers 0 quand n tend vers l'infini. Prélevons dans chaque
une famille décroissante de fermés dont le diamêtre tend vers 0 quand n tend vers l'infini. Prélevons dans chaque 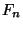 un élément
un élément 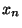 et montrons que la suite ainsi construite est de Cauchy. Soit
et montrons que la suite ainsi construite est de Cauchy. Soit
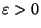 . Comme
. Comme
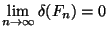 , il existe N dans INtel que si n>N alors
, il existe N dans INtel que si n>N alors
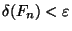 . Mais donc, par définition du diamêtre, si n et m sont plus grands que N, d(
. Mais donc, par définition du diamêtre, si n et m sont plus grands que N, d(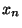 ,
,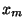 )<
)<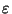 , ce qui prouve bien que la suite est de Cauchy. Mais (X,d) étant complet, elle converge vers un élément x de X.
, ce qui prouve bien que la suite est de Cauchy. Mais (X,d) étant complet, elle converge vers un élément x de X.
Il reste à montrer que x est dans l'intersection des 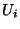 . Supposons que ce ne soit pas le cas. Il existerait alors i dans INtel que x ne soit pas élément de
. Supposons que ce ne soit pas le cas. Il existerait alors i dans INtel que x ne soit pas élément de 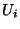 . Mais
. Mais 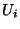 étant fermé dans un espace complet, il est complet pour la distance induite. Donc la suite
étant fermé dans un espace complet, il est complet pour la distance induite. Donc la suite
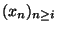 qui est incluse dans
qui est incluse dans 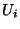 et qui est de Cauchy pour la distance induite
et qui est de Cauchy pour la distance induite  sur
sur 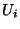 converge dans
converge dans 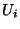 . Donc sa limite x est élément de
. Donc sa limite x est élément de 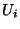 ce qui est en contradiction avec notre hypothèse de départ. Donc x est dans l'intersection des
ce qui est en contradiction avec notre hypothèse de départ. Donc x est dans l'intersection des 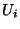 .
.
Proposition Tout produit fini d'espaces métriques (X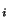 ,d
,d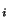 ) où
) où 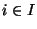 (et où I est un ensemble fini) complets est complet pour la métrique produit
(et où I est un ensemble fini) complets est complet pour la métrique produit  (si x=
(si x=
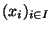 et y=
et y=
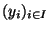 , d(x,y)=sup
, d(x,y)=sup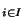 d
d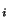 (
(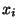 ,
,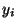 )).
)).
Démonstration Soit
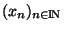 une suite de Cauchy de
une suite de Cauchy de
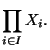 Notons
Notons
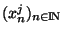 la j
la j
 suite coordonnée. Comme
suite coordonnée. Comme
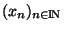 est de Cauchy pour d, pour
est de Cauchy pour d, pour
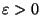 donné, il existe N dans INtel que quelque soient
donné, il existe N dans INtel que quelque soient 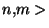 N, on a d
N, on a d
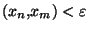 . Par definition de la métrique produit
. Par definition de la métrique produit  , cela implique, pour chacune des suites coordonnées: si
, cela implique, pour chacune des suites coordonnées: si 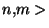 N, on a d
N, on a d
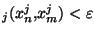 . Donc la j
. Donc la j
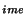 suite coordonnée est de Cauchy dans (X
suite coordonnée est de Cauchy dans (X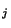 ,d
,d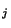 ) et ce pour tout j dans I. Comme chaque (X
) et ce pour tout j dans I. Comme chaque (X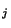 ,d
,d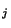 ) est complet, chaque suite coordonnees
) est complet, chaque suite coordonnees
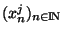 converge vers un élément x
converge vers un élément x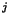 de X
de X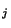 . Montrons maintenant que la suite
. Montrons maintenant que la suite
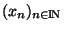 converge vers x=
converge vers x=
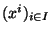 . Soit
. Soit 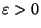 . Pour tout i dans I, on peut trouver N
. Pour tout i dans I, on peut trouver N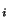 tel que si n>N
tel que si n>N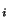 alors
alors
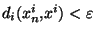 . Posons N=
. Posons N=
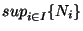 . Pour ce N là et par definition de la métrique produit
. Pour ce N là et par definition de la métrique produit  , on a: si n>N
, on a: si n>N
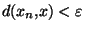 .
.
Proposition IR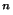 muni de la métrique produit est complet.
muni de la métrique produit est complet.
Proposition Tout espace métrique compact (X,d)  est complet.
est complet.
Démonstration Soit (X,d) un espace métrique compact  et soit
et soit
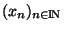 une suite de Cauchy de X.
une suite de Cauchy de X.
Remarquons que si une suite de Cauchy possède une sous suite convergente  , alors elle est convergente: Soient
, alors elle est convergente: Soient
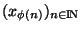 une sous suite convergente de
une sous suite convergente de
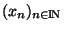 et x sa limite. Soit aussi
et x sa limite. Soit aussi 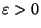 et
et
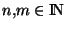 . On a, en utilisant l'inégalité triangulaire
. On a, en utilisant l'inégalité triangulaire  ,
,
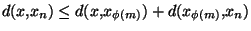 . Mais, comme
. Mais, comme
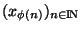 converge vers x
converge vers x  , il existe
, il existe
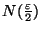 tel que si
tel que si
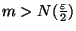 alors
alors
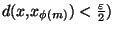 . De plus, comme
. De plus, comme
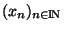 est de Cauchy, il existe
est de Cauchy, il existe
 tel que si n et m sont plus grands que
tel que si n et m sont plus grands que
 alors
alors
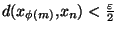 . Mais alors,
. Mais alors,
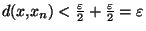 , et ce dés que
, et ce dés que 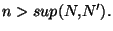
Nous sommes maintenant en mesure de traiter la démonstration de notre prop.: Comme (X,d) est un espace métrique compact, la propriété de Bolzano-Weierstrass  nous autorise à affirmer que la suite de Cauchy
nous autorise à affirmer que la suite de Cauchy
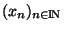 possède une sous suite convergente et donc, d'après la remarque précédente, qu'elle est convergente.
possède une sous suite convergente et donc, d'après la remarque précédente, qu'elle est convergente.



suivant: Théorème du point fixe
monter: Espaces métriques complets
précédent: Notions de base
Emmanuel_Vieillard-Baron_pour_les.mathematiques
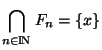 .
.
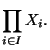 Notons
Notons