


monter: Espaces métriques complets
précédent: Théorème du point fixe
Définition On dit qu'un espace topologique (Y,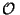 ) (ou un espace métrique (Y,d))est de Baire si pour toute famille d'ouvert
) (ou un espace métrique (Y,d))est de Baire si pour toute famille d'ouvert
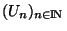 de Y vérifiant:
de Y vérifiant:
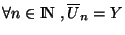
 , alors
, alors
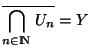
 .
Remarque Cela revient à dire que (Y,
.
Remarque Cela revient à dire que (Y,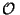 ) est de baire si pour toute famille de fermé d'intérieur vide
) est de baire si pour toute famille de fermé d'intérieur vide  alors la réunion de ces fermés est encore d'intérieur vide.
alors la réunion de ces fermés est encore d'intérieur vide.
Théorème (de Baire) Si (X,d) est un espace métrique complet alors il est de Baire.
Démonstration Soit
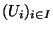 vérifiant:
vérifiant:
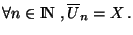 Montrons que l'intersection de tout les éléments de cette famille est dense
Montrons que l'intersection de tout les éléments de cette famille est dense  dans X. Soit x un élément de X. Comme
dans X. Soit x un élément de X. Comme 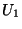 est dense
est dense  dans X, pour tous
dans X, pour tous 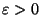 ,
,
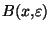
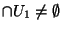
 . Fixons donc
. Fixons donc 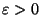 .Comme cette intersection est ouverte (intersection de deux ouverts
.Comme cette intersection est ouverte (intersection de deux ouverts  ), Il existe
), Il existe 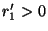 et
et 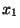 dans X tel que
dans X tel que
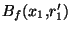
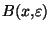
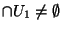
 . Posons
. Posons 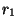 =inf(
=inf(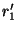 ,
,
 ). On a donc
). On a donc
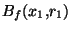
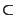
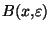
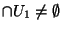 . Supposons cette construction faite à l'ordre n, c'est à dire que l'on suppose trouvés n points
. Supposons cette construction faite à l'ordre n, c'est à dire que l'on suppose trouvés n points 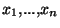 de X et n rééls strictement positifs
de X et n rééls strictement positifs  tels que pour tout i dans
tels que pour tout i dans
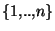 ,
,
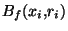
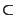
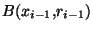
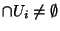 et
et
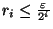 (On pose
(On pose
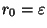 ). Montrons que l'on peut la continuer à l'ordre n+1. Comme
). Montrons que l'on peut la continuer à l'ordre n+1. Comme 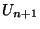 est dense dans X,
est dense dans X, 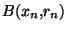
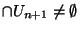 . Mais, comme précedemment, cette intersection est un sous ensemble ouvert de X. On peut donc trouver
. Mais, comme précedemment, cette intersection est un sous ensemble ouvert de X. On peut donc trouver 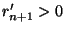 tel que
tel que
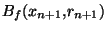
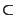
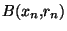
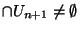 . Posons enfin
. Posons enfin 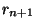 =inf(
=inf(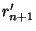 ,
,
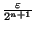 ) et on a bien effectué la construction voulue.
) et on a bien effectué la construction voulue.
Remarquons maintenant que la famille
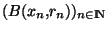 est une suite décroissante de fermé dont le diamètre
est une suite décroissante de fermé dont le diamètre  tend vers 0 quand n tend vers l'infini. Comme X est complet, ceci implique que
tend vers 0 quand n tend vers l'infini. Comme X est complet, ceci implique que
 est un singleton
est un singleton
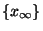 où
où 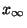 est élément de X
est élément de X  . Mais
. Mais 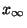 est, par constuction élément de
est, par constuction élément de
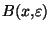 et de
et de
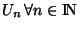 . Donc
. Donc
ce qui implique que
et comme x et 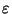 sont arbitraires, que
sont arbitraires, que
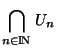 est dense dans X.
est dense dans X.



monter: Espaces métriques complets
précédent: Théorème du point fixe
Emmanuel_Vieillard-Baron_pour_les.mathematiques
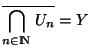
 est un singleton
est un singleton
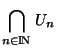 est dense dans X.
est dense dans X.