next up previous
suivant: Propriétés monter: Espaces métriques complets précédent: Introduction

Notions de base

Dans tous ce chapitre (X,d) désignera un espace métrique .
Définition On dira que la suite 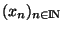$(x_n)_{\scriptsize {n \in {\rm I\!N }}}$ est de Cauchy dans X si elle vérifie:

\begin{displaymath}\forall \varepsilon>0 \exists N \in {\rm I\!N } \forall n,m>N d(x_n,x_m)<\varepsilon\end{displaymath}

Proposition Remarquons qu'une suite de Cauchy n'est pas nécessairement convergente mais qu'une suite convergente est toujours de Cauchy. D'ailleurs:
Définition Un espace métrique sur lequel les suites de Cauchy sont convergentes sera appelé espace complet.
Exemple (IR,| |) est un espace complet.
Exemple Sur (IQ,| |), on définit la suite suivante:

\begin{displaymath}Soit a \in {\rm I\!R }^{+*} u_0=1 et \forall n>0 u_{n+1}={1\over 2}(u_n+{a \over u_n})\end{displaymath}

Cette suite est de Cauchy sur IQet converge vers 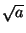$\sqrt{a}$, donc diverge dans IQ.
Remarque Ajoutons que cette notion de complétude dépend complètement de la métrique choisie pour l'espace et pas du tout de sa topologie. Ainsi, il est possible d'exhiber des espaces munis de deux métriques différentes et qui induiront des topologies équivalentes . Par contre, pour une des deux métriques les suites de Cauchy convergeront, ce qui ne sera pas le cas pour l'autre. En l'occurence, on a la propriété suivante.
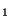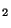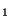Proposition Soient X un espace et d$_1$,d$_2$ deux métriques équivalentes sur X. Alors si (X, d$_1$) est complet, il en est de même de (X,d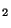$_2$).De plus, toute suite de Cauchy convergente pour l'un est suite de Cauchy convergente pour l'autre.
Définition On dira d'une partie U de X qu'elle est un sous espace complet de X si elle est complète pour la métrique induite de celle de X.
next up previous
suivant: Propriétés monter: Espaces métriques complets précédent: Introduction
Emmanuel_Vieillard-Baron_pour_les.mathematiques