suivant: Compacité et topologie métrique monter: Espaces métriques compacts précédent: Sous espaces métrique compacts

Continuité et compacité

Théorème fondamental L'image d'un compact par une application continue

est compacte.
Démonstration Soient K un compact de (X,d), (Y,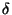 $\delta$ ) un espace métrique et 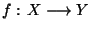$f: X\longrightarrow Y$ une application continue de X dans Y. Soit 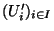$(U_i')_{\scriptsize {i \in I}}$ un recouvrement ouvert de

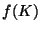(pour la métrique induite sur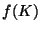

...). On a donc

$\begin{displaymath}f(K)=\displaystyle{\bigcup_{i \in I} U_i}.\end{displaymath}$

Rappelons que si A et B désignent deux ensembles quelconques de Y alors

$\begin{displaymath}f^{-1}(A \cup B)\subset f^{-1}(A) \cup f^{-1}(B).\end{displaymath}$

Alors

$\begin{displaymath}K \subset f^{-1}(f(K)) \subset \displaystyle{f^{-1}(\bigcup_{i \in I} U_i)\subset \bigcup_{i \in I}f^{-1}(U_i)}.\end{displaymath}$

Mais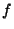

étant continue, chaque 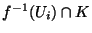$f^{-1}(U_i)\cap K$ est un ouvert de K

(pour la métrique induite

de X sur K).Comme K est compact

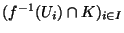, on peut extraire de la famille $(f^{-1}(U_i)\cap K)_{\scriptsize {i \in I}}$ un recouvrement fini de K 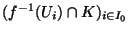$(f^{-1}(U_i)\cap K)_{\scriptsize {i \in I_0}}$ (où I

est une sous partie finie de I). On a alors, comme

$\begin{displaymath}f(A)\cup f(B)=f(A\cup B),\end{displaymath}$

$\begin{displaymath}f(K)\subset \displaystyle{f(\bigcup_{i \in I_0}f^{-1}( U_i)\c... ...cup_{i \in I_0}f(f^{-1}( U_i))\subset \bigcup_{i \in I_0} U_i}.\end{displaymath}$

Et donc, du recouvrement initial de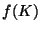

, on a extrait un recouvrement fini, ce qui prouve que

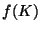est compact

.
Théorème fondamental On considère (IR,| |). Soit 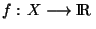$f: X\longrightarrow {\rm I\!R }$ une application continue

de X dans IR. Et soit K un compact de X. Alors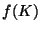

est bornée

dans IRet f atteind ses bornes sur K.
Démonstration Comme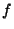

est continue et que K est compact,

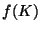est compact dans IR

. Mais comme tout compact d'un espace métrique est un sous ensemble borné de cet espace métrique

, on en déduit que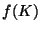

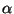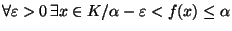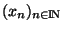est borné dans IR. Mais tout ensemble borné de IRpossède une borne supérieur (et une borne inférieur). Notons $\alpha$ sa borne sup. On peut alors écrire: $\forall \varepsilon >0 \exists x \in K / \alpha-\varepsilon<f(x) \leq \alpha$ . 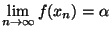En remplaçant $\varepsilon$ par ${1 \over n}$ et ce pout tout n dans IN $^\ast$ , on construit une suite $(x_n)_{\scriptsize {n \in {\rm I\!N }}}$ de K telle que: $\displaystyle{\lim_{n\rightarrow \infty}f(x_n)=\alpha}$

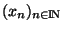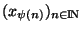
. Mais la suite $(x_n)_{\scriptsize {n \in {\rm I\!N }}}$ , étant incluse dans un compact, possède une suite extraite convergente $(x_{\psi(n)})_{\scriptsize {n \in {\rm I\!N }}}$

et si nous notons x sa limite, x est élément de K. Par continuité de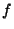

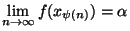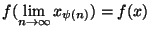
, on a $\displaystyle{\lim_{n\rightarrow \infty}f(x_{\psi(n)})=\alpha}$ = $f(\displaystyle{\lim_{n\rightarrow \infty} x_{\psi(n)}})=f(x)$

et donc f atteind bien son maximum en un point de K. On pourrait procéder de même avec la borne inférieure.
Théorème ( de Heine ) On considère encore deux espaces métriques (X,d) et (Y,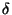 $\delta$ ). On suppose aussi que X est compact. Soit 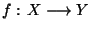$f: X\longrightarrow Y$ une application continue de X dans Y. Alors

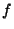est uniformément continue

.
Démonstration Soit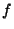

comme dans l'énoncé du théorème Supposons que

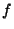ne soit pas uniformément continue

sur X (mais seulement continue

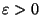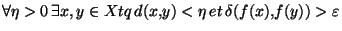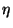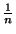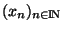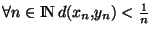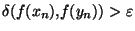). Alors il existe $\varepsilon>0$ tel que $\forall \eta>0 \exists x, y \in X tq d(x,y)<\eta et \delta(f(x),f(y))>\varepsilon$ . En particulier, en remplaçant $\eta$ par ${1 \over n}$ , on construit deux suites $(x_n)_{\scriptsize {n \in {\rm I\!N }}}$ et $(y_n)_{\scriptsize {n \in {\rm I\!N }}}$ telles que $\forall n \in {\rm I\!N }d(x_n,y_n)<{1 \over n}$ et $\delta(f(x_n),f(y_n))>\varepsilon$ . 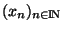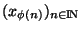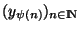Comme X est compact, $(x_n)_{\scriptsize {n \in {\rm I\!N }}}$ et $(y_n)_{\scriptsize {n \in {\rm I\!N }}}$ possèdent des sous suites convergentes $(x_{\phi(n)})_{\scriptsize {n \in {\rm I\!N }}}$ et $(y_{\psi(n)})_{\scriptsize {n \in {\rm I\!N }}}$ dans X

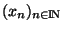. Soient x et y les limites respectives de ces deux sous suites. Par construction des suites $(x_n)_{\scriptsize {n \in {\rm I\!N }}}$ et $(y_n)_{\scriptsize {n \in {\rm I\!N }}}$ , on peut affirmer que x=y. De plus , comme f est continue et que l'application 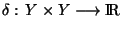$\delta: Y\times Y\longrightarrow {\rm I\!R }$ est continue, l'application 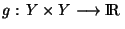$g: Y\times Y\longrightarrow {\rm I\!R }$ définie par 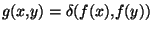$g(x,y)=\delta(f(x),f(y))$ est continue

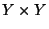sur $Y\times Y$ muni de la topologie produit

et on peut écrire

$\begin{displaymath}\displaystyle{\lim_{n \rightarrow \infty} \delta(f(x_{\phi(n)... ..._{\psi(n)}))=\delta(f(x),f(y))=\delta(f(x),f(x))=0>\varepsilon}\end{displaymath}$

ce qui est en contradiction avec notre choix de 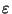$\varepsilon$ . Donc, f est bien uniformément continue.

suivant: Compacité et topologie métrique monter: Espaces métriques compacts précédent: Sous espaces métrique compacts

Emmanuel_Vieillard-Baron_pour_les.mathematiques