suivant: Continuité et compacité monter: Espaces métriques compacts précédent: Suites dans un espace

Sous espaces métrique compacts

Définition On dit d'un sous ensemble de (X, $\cal{O}$ ) qu'il est compact s'il est compact pour la métrique induite

de celle de X.
Remarque Afin de simplifier l'utilisation des sous espaces compacts, on donne la caractérisation suivante:
Proposition On a équivalence entre:

K est un sous espace compact de X.
Pour toute famille $(U_i)_{\scriptsize {i \in I}}$ d'ouverts de X tel que

$\begin{displaymath}K \subset \displaystyle{\bigcup_{i _in I} U_i},\end{displaymath}$

il existe I $_0\subset I$ de cardinal fini tel que

$\begin{displaymath}K \subset \displaystyle{\bigcup_{i _in I_0} U_i}.\end{displaymath}$

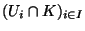Démonstration Si $(U_i)_{\scriptsize {i \in I}}$ est une famille d'ouverts de X, alors $(U_i\cap K)_{\scriptsize {i \in I}}$ est une famille d'ouverts de K pour la métrique induite

de X sur K. Si K est compact

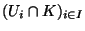, et que $(U_i\cap K)_{\scriptsize {i \in I}}$ est un recouvrement ouvert

de K, on peut en extraire un recouvrement fini et on aura nécessairement

$\begin{displaymath}K \subset \displaystyle{\bigcup_{i \in I_0} U_i}\end{displaymath}$

où I

désigne une sous partie finie de I. Réciproquement, si pour toute famille $(U_i)_{\scriptsize {i \in I}}$ vérifiant

$\begin{displaymath}K \subset \displaystyle{\bigcup_{i _in I} U_i},\end{displaymath}$

on peut extaire une sous famille finie recouvrant K alors cela prouve que pour toute famille d'ouvert de K (pour la métrique induite de X sur K) et recouvrant K, on peut extraire une sous famille finie recouvrant K. K est donc compact pour la métrique induite.
Théorème Tout compact est fermé.
Démonstration Soit K un compact de X.(On peut avoir K=X).Montrons que K

est ouvert

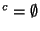. Si K $^c=\emptyset$ alors la dém. est terminée. Sinon soit 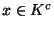$x\in K^c$ . Comme X est un espace séparé

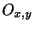, pour tout y dans K, on peut trouver un ouvert $O_{x,y}$ contenant x et un ouvert

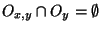contenant y tel que $O_{x,y}\cap O_y=\emptyset$ . Mais on a l'inclusion

$\begin{displaymath}K\subset \displaystyle{\bigcup_{y \in K} O_y}.\end{displaymath}$

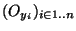
La famille $(O_y)_{\scriptsize {y \in K}}$ definit donc un recouvrement ouvert de K. De ce recouvrement, on peut extraire un recouvrement fini $(O_{y_i})_{\scriptsize {i \in 1..n}}$

. Posant

$\begin{displaymath}O=\displaystyle{\bigcap_{i=1}^n O_{x,y_i}}\end{displaymath}$

(qui est ouvert comme intersection finie d'ouverts

), on construit un ouvert de O contenant x et disjoint de K. On montre ainsi bien que K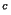

est ouvert et donc que K est fermé

.
Théorème Tout fermé dans un compact est compact.
Démonstration Soient F un fermé et K un compact de X contenant F. Soit aussi $(U_i)_{\scriptsize {i \in I}}$ une famille d'ouverts (ouverts pour la topologie de K) dont la réunion contient K. La famille 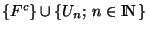$\lbrace F^c \rbrace \cup \lbrace U_n ; n\in {\rm I\!N }\rbrace$ est un recouvrement ouvert de K. On peut donc en extraire un recouvrement fini de K 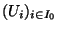$(U_i)_{\scriptsize {i \in I_0}}$ ou I

est une partie finie de I

. Mais alors

$\begin{displaymath}F \subset \displaystyle{\bigcup_{i \in I_0} U_i},\end{displaymath}$

et F est compact Cqfd.
Théorème Tout compact est borné

.
Démonstration Supposons que K, compact de (X,d) ne soit pas borné

. Soit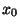

un élément de K. Pour tout n $\in$ IN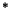 $^\ast$ , il existe un élément

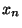de K appartenant à l'ensemble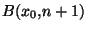

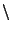
$\setminus$

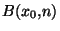. La suite ainsi construite vérifie 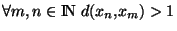$\forall m, n \in {\rm I\!N } d(x_n,x_m)>1$ et ne peut avoir de suite extraite convergente atomamm15. Ceci rentre en contradiction avec le théorème de Bolzano-Weierstrass

et prouve notre théorème
Proposition

Une réunion finie de sous espaces compacts est compacte.
Une intersection quelconque de sous espaces compacts est compacte.

Démonstration

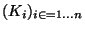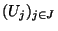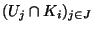Soit $(K_i)_{\scriptsize {i \in =1...n}}$ une famille finie de sous espaces compacts. Soit K la réunion des éléments de cette famille et $(U_j)_{\scriptsize {j \in J}}$ un recouvrement ouvert de K. Pour tout i=1...n, $(U_j\cap K_i)_{\scriptsize {j \in J}}$ est donc un recouvrement ouvert de K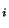. Mais comme chaque K 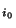$_{i_0}$ est compact , pour tout 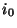=1...n, on peut trouver un sous-ensemble fini J 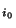$_{i_0}$ de J tel que K 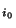$_{i_0}$ soit recouvert par la famille finie d'ouverts 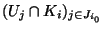$(U_j\cap K_i)_{\scriptsize {j \in J_{i_0}}}$ . Mais la famille 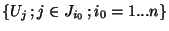$\lbrace U_j ; j\in J_{i_0} ;i_0=1...n \rbrace$ est finie, extraite de la famille 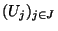$(U_j)_{\scriptsize {j \in J}}$ et recouvre K. D'un recouvrement quelconque de K, on a extrait un recouvrement fini et on a ainsi bien montré que K est compact .
Soit 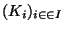$(K_i)_{\scriptsize {i \in \in I}}$ une famille finie de sous espaces compacts. Cette fois ci K désignera l'intersection des éléments de cette famille. Remarquons tout d'abord que K est fermé comme intersection quelconque de fermés . De plus, pour tout i dans I, K est inclus dans K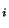. Donc K est un sous ensemble fermé d'un espace compact . C'est donc un espace compact.

suivant: Continuité et compacité monter: Espaces métriques compacts précédent: Suites dans un espace

Emmanuel_Vieillard-Baron_pour_les.mathematiques