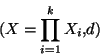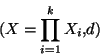next up previous
monter: Espaces métriques compacts précédent: Continuité et compacité

Compacité et topologie métrique produit

Théorème (de Tychonov) Un produit fini d'espace métrique compact est compact pour la métrique produit .
Démonstration On considère la famille d'espace métrique 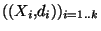$((X_i,d_i))_{\scriptsize {i =1..k}}$ et

\begin{displaymath}\displaystyle{(X=\prod_{i=1}^k X_i,d)}\end{displaymath}

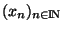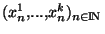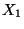où d désigne la métrique produit. Il s'agit donc de montrer que (X,d) est compact. Pour ce faire, nous allons considérer une suite $(x_n)_{\scriptsize {n \in {\rm I\!N }}}$= $(x_n^1,...,x_n^k)_{n \in {\rm I\!N }}$ de X et montrer qu'elle possède une sous suite convergente , ce qui, d'après le théorème de Bolzano-Weierstrass , nous permettra de conclure. 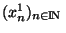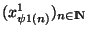Tout d'abord, comme $X_1$ est compact, de la suite $(x^1_n)_{\scriptsize {n \in {\rm I\!N }}}$, on peut extraire une sous suite convergente $(x_{\psi 1(n)}^1)_{\scriptsize {n \in {\rm I\!N }}}$ . 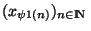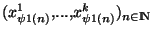La suite $(x_{\psi 1(n)})_{\scriptsize {n \in {\rm I\!N }}}$= $(x_{\psi 1(n)}^1,...,x_{\psi 1(n)}^k)_{n \in {\rm I\!N }}$ est donc une suite extraite de 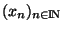$(x_n)_{\scriptsize {n \in {\rm I\!N }}}$ et la première suite coordonnée de cette suite est convergente. Remarquons aussi que toute suite extraite d'une suite convergente est convergente et converge vers la même limite que la suite de départ. La suite 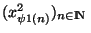$(x_{\psi 1(n)}^2)_{\scriptsize {n \in {\rm I\!N }}}$ est une suite de $X_2$ et possède donc une sous suite convergente. 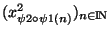Cette sous suite est de la forme $(x_{\psi 2 \circ \psi 1(n)}^2)_{\scriptsize {n \in {\rm I\!N }}}$. De plus d'après la remarque précédente, la suite 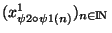$(x_{\psi 2 \circ \psi 1(n)}^1)_{\scriptsize {n \in {\rm I\!N }}}$ est une suite extraite de 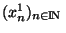$(x^1_n)_{\scriptsize {n \in {\rm I\!N }}}$ et convergeant dans 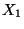$X_1$. La suite 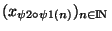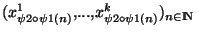$(x_{\psi 2 \circ \psi 1(n)})_{\scriptsize {n \in {\rm I\!N }}}$= $(x_{\psi 2 \circ \psi 1(n)}^1,...,x_{\psi 2 \circ \psi 1(n)}^k)_{n \in {\rm I\!N }}$ est donc une suite extraite de 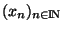$(x_n)_{\scriptsize {n \in {\rm I\!N }}}$. De plus, les deux première suites coordonnées de cette suite sont convergentes. Un raisonement par récurrence nous permet encore de trouver k-2 applications 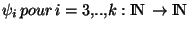$\psi_i pour i=3,..,k:{\rm I\!N }\rightarrow {\rm I\!N }$, telles que 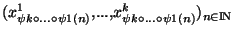$(x_{\psi k \circ ... \circ \psi 1(n)}^1,...,x_{\psi k \circ ... \circ \psi 1(n)}^k)_{n \in {\rm I\!N }}$ est une suite extraite de 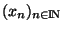$(x_n)_{\scriptsize {n \in {\rm I\!N }}}$ et pour laquelle toutes les suites coordonnées sont des suites convergentes. Cette suite extraite est donc convergente , Cqfd.
Remarque Ce théorème est encore vrai dans le cas où le produit est dénombrable.
next up previous
monter: Espaces métriques compacts précédent: Continuité et compacité
Emmanuel_Vieillard-Baron_pour_les.mathematiques