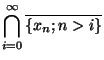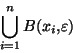suivant: Sous espaces métrique compacts
monter: Espaces métriques compacts
précédent: Notions de base
Proposition Si (X,d) est un espace métrique compact, alors toute suite de X possède un point d'accumulation  .
.
Démonstration En effet, on a vu dans le cours sur les espaces métriques que l'ensemble des points d'accumulation d'une suite
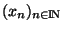 est donné par
est donné par
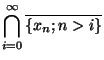
 . Posons
. Posons
La famille 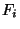 est bien une suite décroissante de fermés
est bien une suite décroissante de fermés  non vides. Et donc, par application de la proposition précédente, l'intersection de tous les éléments de cette famille est non vide. L'ensemble des points d'accumulation de la suite
non vides. Et donc, par application de la proposition précédente, l'intersection de tous les éléments de cette famille est non vide. L'ensemble des points d'accumulation de la suite
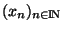 est par conséquent non vide. Cqfd.
est par conséquent non vide. Cqfd.
En utilisant la proposition  , on peut encore exprimer la proposition précédente sous la forme:
, on peut encore exprimer la proposition précédente sous la forme:
Proposition (X,d) est un espace métrique compact alors toute suite
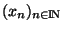 de X possède une sous-suite convergente
de X possède une sous-suite convergente  .
.
On peut donc affirmer que toute suite dans un espace métrique compact possède une sous suite convergente.
Remarque On pourrait se poser le problème de la réciproque. Donnons nous (X,d) un espace métrique ayant la propriété : De toutes suites de X, on peut extraire une suite convergente. Peut on alors affirmer que (X,d) est compact? La réponse est positive et est donnée pas le Théorème de Bolzano-Weierstrass.
Théorème (de Bolzano-Weierstrass) On a équivalence entre:
- (X,d) est compact.
- De toute suite de (X,d), on peut extraire une sous-suite
 convergente
convergente  dans X.
dans X.
Démonstration Le sens direct vient d'être prouvé. Pour la réciproque, la dém. se décompose en deux lem mes.: On considère donc un espace métrique (X,d) tel que de toute suite de X, on peut extraire une sous-suite convergente.
Lemme 1 Pour tout 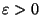 , on peut recouvrir X par un nombre fini de boules de rayon
, on peut recouvrir X par un nombre fini de boules de rayon 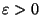
 .
.
Démonstration
Supposons qu'il existe 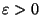 tel que ce ne soit pas possible. Choisissons alors
tel que ce ne soit pas possible. Choisissons alors 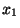 dans X.
dans X.
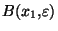
 ne recouvre pas X
ne recouvre pas X  . On peut donc trouver
. On peut donc trouver 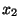 dans X n'appartenant pas à
dans X n'appartenant pas à
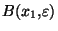 . Supposons construit une famille
. Supposons construit une famille
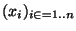 de point de X tel que
de point de X tel que
ne recouvre pas X  . On peut alors trouver
. On peut alors trouver 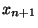 dans X n'appartenant pas à cette réunion et tel que la famille (
dans X n'appartenant pas à cette réunion et tel que la famille (
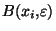
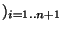 ne recouvre toujours pas X. On construit ainsi une suite
ne recouvre toujours pas X. On construit ainsi une suite
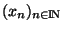 de X tel que, pour tout i, j
de X tel que, pour tout i, j  INd(
INd(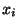 ,
,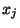 )>
)>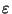 . Cette suite ne peut, par conséquent, avoir une sous-suite convergente
. Cette suite ne peut, par conséquent, avoir une sous-suite convergente  . Ceci prouve le lem me par l'absurde.
. Ceci prouve le lem me par l'absurde.
Lemme 2 Donnons nous un recouvrement ouvert

 de X. Il existe r>0 tel que
de X. Il existe r>0 tel que
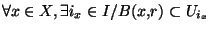
 .
.
Démonstration Raisonnons à nouveau par l'absurde et suppososons que pour tout r>0, il existe 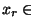 X tel que
X tel que 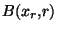
 n'est incluse dans aucun des
n'est incluse dans aucun des 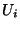 où
où 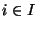 . En particulier, pout tout n dans IN, on peut trouver
. En particulier, pout tout n dans IN, on peut trouver 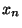 tel que
tel que
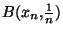 n'est incluse dans aucun des
n'est incluse dans aucun des 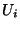 où
où 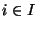 . Cette suite
. Cette suite
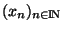 doit posséder, par hypothèse, une sous suite
doit posséder, par hypothèse, une sous suite  convergente
convergente 
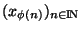 . Notons x
. Notons x  X sa limite
X sa limite  .(x est donc aussi valeur d'adhérence
.(x est donc aussi valeur d'adhérence  de
de
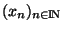 ). Mais comme
). Mais comme
 est un recouvrement ouvert
est un recouvrement ouvert  de X, il existe
de X, il existe 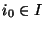 tel que
tel que  . L'ouvert
. L'ouvert 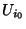 est donc un voisinage
est donc un voisinage  de x. Par définition de la limite d'une suite
de x. Par définition de la limite d'une suite  : pour tout
: pour tout 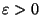 , il existe N
, il existe N
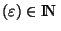 tel que
tel que
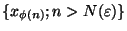 est inclus dans
est inclus dans
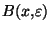 . Comme
. Comme 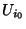 est ouvert, on peut choisir
est ouvert, on peut choisir 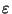 assez petit en sorte que
assez petit en sorte que
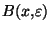 soit contenue dans
soit contenue dans 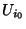 . Soit
. Soit 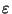 ainsi choisis. Si
ainsi choisis. Si
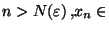
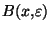 . De plus, si n est assez grand, on a même:
. De plus, si n est assez grand, on a même:
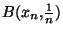
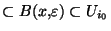 , ce qui contredit notre hypothèse de départ. Cqfd.
, ce qui contredit notre hypothèse de départ. Cqfd.
Démontrons enfin le théorème de Bolzano-Weierstrass. Choisissons un recouvrement

 de X. On sait, d'après le second lem me
de X. On sait, d'après le second lem me  , qu'il existe un réél r>0 tel que pour tout x,
, qu'il existe un réél r>0 tel que pour tout x,  soit incluse dans l'un des
soit incluse dans l'un des 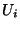 . Le lem me 1
. Le lem me 1  appliqué dans le cas où
appliqué dans le cas où 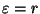 nous permet d'affirmer l'existence d'une famille
nous permet d'affirmer l'existence d'une famille
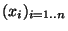 de points de X tels que
de points de X tels que
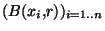
 recouvre X. Mais pour tout k=1..n, il existe
recouvre X. Mais pour tout k=1..n, il existe 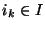 tel que
tel que 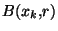
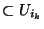 . La famille
. La famille
 recouvre alors X et du recouvrement initial, on a bien extrait un recouvrement fini
recouvre alors X et du recouvrement initial, on a bien extrait un recouvrement fini  .
.
Définition Le nombre r s'appelle le nombre de Lebesgue du recouvrement
 .
.



suivant: Sous espaces métrique compacts
monter: Espaces métriques compacts
précédent: Notions de base
Emmanuel_Vieillard-Baron_pour_les.mathematiques