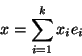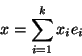suivant: Applications linéaires
monter: Espaces vectoriels normés
précédent: Espaces vectoriels normés de
Les propriétés qui viennent découlent de l'équivalence des normes . On considère encore ici un k-espace vectoriel E de dimension finie n.
. On considère encore ici un k-espace vectoriel E de dimension finie n.
Corollaire Pour toute norme  sur E et toute norme
sur E et toute norme  ' sur k
' sur k , il existe un isomorphisme bicontinue entre (E,
, il existe un isomorphisme bicontinue entre (E, ) et (k
) et (k ,
, ').
').
Démonstration Il suffit de fixer une base
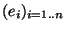 dans E et de considérer l'application
dans E et de considérer l'application 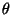 qui à un vecteur x de E lui associe ses coordonnées dans k
qui à un vecteur x de E lui associe ses coordonnées dans k . Cette aplication est clairement un isomorphisme et est bicontinue ( c'est une isométrie!!!) pour la norme infinie de E et la métrique produit
. Cette aplication est clairement un isomorphisme et est bicontinue ( c'est une isométrie!!!) pour la norme infinie de E et la métrique produit  sur k
sur k , comme nous l'avons démontré au début de cette section
, comme nous l'avons démontré au début de cette section . Comme de plus, toutes les normes sur E, ainsi que sur k
. Comme de plus, toutes les normes sur E, ainsi que sur k , sont équivalentesatomaevc5, notre isomorphisme est bicontinue de E sur k
, sont équivalentesatomaevc5, notre isomorphisme est bicontinue de E sur k , et ce quelque soient les normes choisies sur E et k
, et ce quelque soient les normes choisies sur E et k .
.
Corollaire Un sous espace de dimension finie d'un evn est complet .
.
Démonstration Soit F un sous espace vectoriel d'un k-evn (X, ) de dimension finie. Considérons la restriction de la norme de X au sous espace F. Cela définie une norme sur F
) de dimension finie. Considérons la restriction de la norme de X au sous espace F. Cela définie une norme sur F  que l'on note
que l'on note 
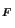 . Comme F est de dimension finie, la norme
. Comme F est de dimension finie, la norme 
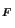 est équivalente
est équivalente , si l'on se fixe une base
, si l'on se fixe une base
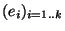 dans F, à la métrique produit sur F
dans F, à la métrique produit sur F . Si une suite
. Si une suite
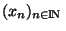 est de Cauchy
est de Cauchy  dans (F,
dans (F,
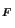 ), alors elle sera de Cauchy dans (F,
), alors elle sera de Cauchy dans (F,
 ) et, si l'on note
) et, si l'on note
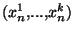 le vecteur coordonné des éléments
le vecteur coordonné des éléments 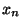 de la suite et ce
de la suite et ce 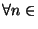 IN, chacune de ces coordonnées, par définition de la métrique produit
IN, chacune de ces coordonnées, par définition de la métrique produit , est de Cauchy dans (k,| |). k étant complet
, est de Cauchy dans (k,| |). k étant complet , ceci implique que chacune des suites coordonnées
, ceci implique que chacune des suites coordonnées
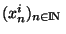 pour i=1...k converge vers un éléments
pour i=1...k converge vers un éléments 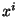 de k
de k . Reste à voir que la suite
. Reste à voir que la suite
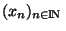 converge vers
converge vers
dans (F,
 ). Il est clair, tout d'abord, que x est élément de F. Fixons ensuite
). Il est clair, tout d'abord, que x est élément de F. Fixons ensuite 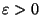 . Comme chaque suite
. Comme chaque suite
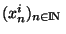 converge vers
converge vers 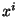 , pour tout i=1..k, on peut trouver
, pour tout i=1..k, on peut trouver
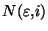 tel que si n>
tel que si n>
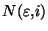 alors
alors
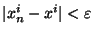
 . Posons alors
. Posons alors
Si n>N
ce qui signifie que
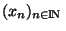 converge vers x pour la métrique produit
converge vers x pour la métrique produit , et donc pour la métrique
, et donc pour la métrique 
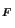 . Ceci implique la complétude de F.
. Ceci implique la complétude de F.
Corollaire Un sous espace de dimension finie d'un evn est fermé .
.
Démonstration Un sous espace de dimension finie d'un evn est un sous espace complet de cet evn . Comme un sous ensemble complet d'un espace métrique est fermé, notre sous espace est fermé
. Comme un sous ensemble complet d'un espace métrique est fermé, notre sous espace est fermé .
.
Corollaire La boule unité  d'un evn de dimension finie est compact
d'un evn de dimension finie est compact  pour la norme de cet evn.
pour la norme de cet evn.
Démonstration On a montré précédemment que la boule unité fermé de (E,
 ): B
): B était compact pour la métrique produit
était compact pour la métrique produit . Elle est donc compact pour toute topologie équivalente à celle induite par la métrique produit. Soit B la boule unité fermé de (E,
. Elle est donc compact pour toute topologie équivalente à celle induite par la métrique produit. Soit B la boule unité fermé de (E, ). Comme les normes
). Comme les normes 
 et
et  sont équivalentes il existe
sont équivalentes il existe 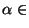 k tel que , pour tout x de E,
k tel que , pour tout x de E, 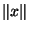
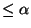
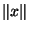

 . Donc B est incluse dans l'image par l'homothétie de rapport
. Donc B est incluse dans l'image par l'homothétie de rapport 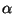 de B
de B :
: 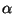 B
B . Mais B
. Mais B est compact dans (E,
est compact dans (E, ) et les homothéties vectorielles
) et les homothéties vectorielles  sont continues dans (E,
sont continues dans (E, ). Comme l'image d'un compact par une application continue est un compact
). Comme l'image d'un compact par une application continue est un compact , on en déduit que
, on en déduit que 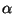 B
B est compact dans (E,
est compact dans (E, ). Mais B etant un sous ensemble fermé de
). Mais B etant un sous ensemble fermé de 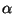 B
B est alors aussi nécessairement compact
est alors aussi nécessairement compact .
.
Remarque La réciproque de ce théorème est vraie et fait l'objet du théorème de Riez qui suit plus loin.
Corollaire Les compacts de E sont les sous ensembles fermés et bornés  de E.
de E.
Démonstration On a déjà montré, dans le chapitre sur les espaces métriques compacts, que tout compact d'un espace métrique est fermé et borné
et borné . Considérons donc maintenant un sous ensemble K fermé et borné de E. Comme K est borné
. Considérons donc maintenant un sous ensemble K fermé et borné de E. Comme K est borné , on peut trouver une boule de centre 0 et de rayon r suffisamment grand pour que cette boule contienne K. L'adhérence
, on peut trouver une boule de centre 0 et de rayon r suffisamment grand pour que cette boule contienne K. L'adhérence de cette boule contiendra donc encore K. Mais cette boule est l'image par l'homothétie de centre 0 et de rapport r de la boule unité fermée de E
de cette boule contiendra donc encore K. Mais cette boule est l'image par l'homothétie de centre 0 et de rapport r de la boule unité fermée de E . Rappelons que l'image d'un compact par une application continue est encore compacte
. Rappelons que l'image d'un compact par une application continue est encore compacte , et donc
, et donc 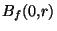 est un compact de (E,
est un compact de (E, ). Mais notre sous ensemble est alors un fermé inclus dans un compact, ce qui implique qu'il est compact
). Mais notre sous ensemble est alors un fermé inclus dans un compact, ce qui implique qu'il est compact .
.
Théorème de Riesz Si la boule unité d'un evn (E, ) est compact alors E est de dimension finie.
) est compact alors E est de dimension finie.
On va, pour la démonstration du théorème, utiliser les notations suivantes: si F et G désignent des parties de E ,que x est élément de E et que 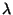 est élément de k,alors:
est élément de k,alors:
 ,
,
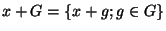 ,
,
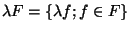 .
.
Démonstration Soit B la boule unité fermé de (E, ) qui est compacte par hypothèse. On note Bo la boule unité ouverte. La famille
) qui est compacte par hypothèse. On note Bo la boule unité ouverte. La famille
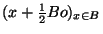 définit un recouvrement ouvert de B
définit un recouvrement ouvert de B . On peut alors en extraire un recouvrement fini
. On peut alors en extraire un recouvrement fini
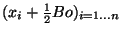 où n est élément de IN
où n est élément de IN amcb3. Soit F le sous espace vectoriel engendré par
amcb3. Soit F le sous espace vectoriel engendré par
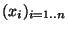 . On a la série d'inclusion: B
. On a la série d'inclusion: B 
 B+F , 2B
B+F , 2B 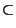 2(
2(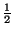 B+F)=B+2F=B+F. Puis 4B
B+F)=B+2F=B+F. Puis 4B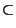 2(B+F)=2B+2F=2B+F=B+B+F. Mais B
2(B+F)=2B+2F=2B+F=B+B+F. Mais B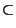 B+F et donc 4B
B+F et donc 4B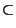 B+F. Par récurence, on montre que 2
B+F. Par récurence, on montre que 2 B
B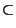 B+F. Mais E=
B+F. Mais E=
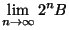 , donc E
, donc E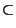 B+F. Supposons que E ne soit pas inclus dans F.
B+F. Supposons que E ne soit pas inclus dans F.
Soit x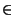 E
E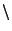 F.Remarquons que F, étant un sous espace vectoriel de dimension finie de E, il est fermé dans E
F.Remarquons que F, étant un sous espace vectoriel de dimension finie de E, il est fermé dans E . Donc, E
. Donc, E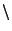 F est ouvert et pour n assez grand, la boule x+
F est ouvert et pour n assez grand, la boule x+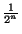 B est incluse dans E
B est incluse dans E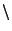 F. C'est à dire (x+
F. C'est à dire (x+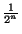 B)
B)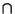 F=
F=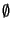 , donc (
, donc (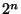 x+B)
x+B)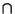 F=
F=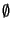 ou encore
ou encore 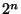 x n'est pas élément de B+F (si
x n'est pas élément de B+F (si 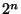 x
x 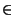 B+F
B+F
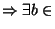 B et
B et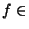 F tel que
F tel que 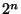 x=
x=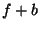 mais alors
mais alors 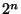 x-
x- ce qui implique que l'intersection de (
ce qui implique que l'intersection de (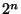 x+B) et F est non vide), ce qui est absurde car on vient d'établir le contraire. Notre hypothèse de départ est donc fausse et E=F, ce qui prouve que E est de dimension finie.
x+B) et F est non vide), ce qui est absurde car on vient d'établir le contraire. Notre hypothèse de départ est donc fausse et E=F, ce qui prouve que E est de dimension finie.



suivant: Applications linéaires
monter: Espaces vectoriels normés
précédent: Espaces vectoriels normés de
Emmanuel_Vieillard-Baron_pour_les.mathematiques