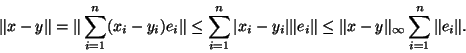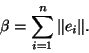suivant: Propriétés des evn de
monter: Espaces vectoriels normés
précédent: Notions de base
Dans ce paragraphe on s'intéresse à un k-espace vectoriel E de dimension finie n.
Définition de la norme infini sur E Choisissons une base
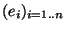 de E. Dans cette base, les vecteurs x de E ont des coordonnées
de E. Dans cette base, les vecteurs x de E ont des coordonnées 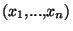 où
où 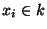 . On définit alors sur E la norme
. On définit alors sur E la norme 
 par
par
où | | désigne l'application valeurs absolue si k=IRet l'application module si k=IC. On vérifie que l'on a bien défini une norme sur E. Cette norme dépend bien évidemment de la base choisie.
Proposition On fixe une base
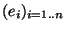 de E. On peut alors introduire la norme
de E. On peut alors introduire la norme 
 sur E. Cette norme est naturellement définie sur k
sur E. Cette norme est naturellement définie sur k . On a alors la propriété suivante:
. On a alors la propriété suivante:
(E,
 ) est homéomorphe
) est homéomorphe  à (k
à (k ,
,
 ). On a même un isomorphisme bicontinue (Cad continue et d'inverse continue) entre ces deux espaces.
). On a même un isomorphisme bicontinue (Cad continue et d'inverse continue) entre ces deux espaces.
Démonstration A tout élément x de E, on associe ses coordonnées dans la base
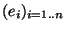 :
: 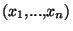 . Cela définit une application
. Cela définit une application
 .
. 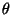 est bien évidemment k-linéaire de E dans k, ainsi que bijective (Unicité des coordonnées d'un vecteur de E dans une base de E). Montrons que
est bien évidemment k-linéaire de E dans k, ainsi que bijective (Unicité des coordonnées d'un vecteur de E dans une base de E). Montrons que 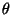 est continue. Soient x et y dans E,
est continue. Soient x et y dans E,
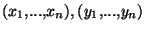 leurs coordonnées respectives . On a, par définition de la norme infinie:
leurs coordonnées respectives . On a, par définition de la norme infinie:
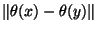
 =
=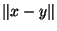
 . Notre isomorphisme
. Notre isomorphisme 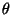 est donc 1-lipschitzien
est donc 1-lipschitzien . Mais cette dernière égalité peut aussi s'écrire :
. Mais cette dernière égalité peut aussi s'écrire :
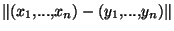
 =
=
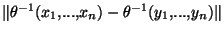
 . Ce qui prouve que
. Ce qui prouve que 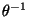 est elle aussi 1-lipschitzienne
est elle aussi 1-lipschitzienne  et donc continue
et donc continue . On a ainsi bien construit un homéomorphisme
. On a ainsi bien construit un homéomorphisme  entre (E,
entre (E,
 ) et (k
) et (k ,
,
 ).
).
Corollaire Ceci a pour conséquence, en particulier, que tout compact  de l'un a pour image un compact de l'autre
de l'un a pour image un compact de l'autre . C'est cette propriété qui va nous être utile dans ce qui suit.
. C'est cette propriété qui va nous être utile dans ce qui suit.
Lemme La boule unité fermée  de (k
de (k ,
,
 ) est un sous espace compact de k
) est un sous espace compact de k
 .
.
Démonstration Notons 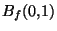 la boule unitée fermée de (k
la boule unitée fermée de (k ,
,
 )
) . On vérifie (voir le cours sur les espaces métriques produits
. On vérifie (voir le cours sur les espaces métriques produits ) que
) que 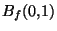 =[-1,1]
=[-1,1] (si k=IR, sinon k=ICet
(si k=IR, sinon k=ICet 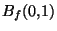 =D(0,1)
=D(0,1)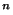 où D(0,1)=
où D(0,1)=
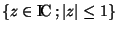 ). Or ([-1,1],| |) est un espace compact ((D(0,1),| |) si k=ICest un espace compact). Mais, d'après le théorème de Tychonov, un produit fini d'espaces compacts est compact pour la topologie produit
). Or ([-1,1],| |) est un espace compact ((D(0,1),| |) si k=ICest un espace compact). Mais, d'après le théorème de Tychonov, un produit fini d'espaces compacts est compact pour la topologie produit  . Donc
. Donc 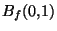 est un sous espace compact de (k
est un sous espace compact de (k ,
,
 ).
).
Lemme La boule unité fermée de (E,
 )
)  est un sous espace compact de E
est un sous espace compact de E .
.
Démonstration Ce sous ensemble de E est l'image par l'application 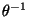 définie dans la démonstration de la proposition précédente de la boule unité fermé de k
définie dans la démonstration de la proposition précédente de la boule unité fermé de k . Mais cette dernière étant compacte et l'application
. Mais cette dernière étant compacte et l'application 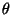 étant un homéomorphisme
étant un homéomorphisme , la boule unité fermée de (E,
, la boule unité fermée de (E,
 ) est nécessairement compact
) est nécessairement compact .
.
Théorème (Equivalence des normes) Soient 
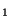 et
et 
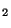 deux normes sur E. Alors ces deux normes sont équivalentes
deux normes sur E. Alors ces deux normes sont équivalentes .
.
Attention, le fait que E soit de dimension finie est ici primordiale.
Démonstration Nous allons en fait travailler avec une norme  de E et montrer qu'elle est équivalente à la norme
de E et montrer qu'elle est équivalente à la norme 
 sur E, une base
sur E, une base
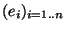 étant fixée sur E. Par transitivité de la relation d'équivalence entre les normes
étant fixée sur E. Par transitivité de la relation d'équivalence entre les normes , on aura ainsi montré que toutes les normes sur E sont équivalentes.
, on aura ainsi montré que toutes les normes sur E sont équivalentes.
Montrons tout d'abord que notre norme  est continue sur (E,
est continue sur (E,
 )
) . Pour cela, prenons x et y dans E. Notons
. Pour cela, prenons x et y dans E. Notons
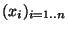 et
et
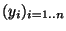 leurs coordonnées respectives dans la base
leurs coordonnées respectives dans la base
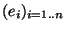 . On a:
. On a:
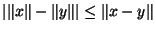 Mais
Mais
Posons alors
L'inégalité se ré-écrit
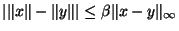 , ce qui prouve que
, ce qui prouve que  est
est 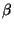 -Lipschitzienne
-Lipschitzienne et donc continue sur (E,
et donc continue sur (E,
 )
) . Ceci prouve, par ailleurs, une des deux inégalités que l'on doit remplir pour vérifier que nos deux normes sont équivalentes
. Ceci prouve, par ailleurs, une des deux inégalités que l'on doit remplir pour vérifier que nos deux normes sont équivalentes .
.
Montrons maintenant la deuxième inégalité. Comme la boule unité fermée de (E,
 ) est compact
) est compact , il en est de même de l'ensemble
, il en est de même de l'ensemble
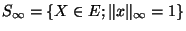 . En effet,
. En effet, 
 est continue sur (E,
est continue sur (E,
 ) et le singleton
) et le singleton
 est un fermé
est un fermé  de IR, donc
de IR, donc 
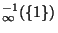 =
=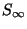 est un fermé de E
est un fermé de E , de plus inclus dans la boule unité de (E,
, de plus inclus dans la boule unité de (E,
 ). Un fermé dans un compact étant compact
). Un fermé dans un compact étant compact , on obtient la propriété voulue.
Mais
, on obtient la propriété voulue.
Mais  est continue et à valeur réelle sur (E,
est continue et à valeur réelle sur (E,
 ). L'ensemble de ses valeurs sur
). L'ensemble de ses valeurs sur 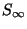 est donc majorée par une constante
est donc majorée par une constante 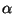
 . On peut écrire :
. On peut écrire :
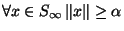 ou encore, par définition de
ou encore, par définition de 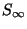 ,
,
Soit encore:
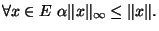 Ce qui nous fournit la seconde inégalité et prouve le théorème.
Ce qui nous fournit la seconde inégalité et prouve le théorème.
Corollaire On a vu dans le chapitre sur les espaces métriques complet que IR était complet pour la métrique produit
était complet pour la métrique produit . Comme la complétude d'un espace métrique est un propriété conservé pour une norme équivalente, on peut affirmer que IR
. Comme la complétude d'un espace métrique est un propriété conservé pour une norme équivalente, on peut affirmer que IR est complet pour n'importe quelle norme.
est complet pour n'importe quelle norme.
Corollaire En particulier, (IC ,
, ) est complet quelque soit la norme
) est complet quelque soit la norme  choisie. En effet, (IC,| |) est complet car par définition IC=IR
choisie. En effet, (IC,| |) est complet car par définition IC=IR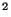 et l'application module corespond à la norme Euclidienne sur IC. Comme IR
et l'application module corespond à la norme Euclidienne sur IC. Comme IR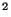 est complet pour la norme Euclidienne
est complet pour la norme Euclidienne , il en de de même de (IC,| |). On en déduit que IC
, il en de de même de (IC,| |). On en déduit que IC est complet pour la métrique produit
est complet pour la métrique produit  et donc pour toute norme sur IC
et donc pour toute norme sur IC .
.



suivant: Propriétés des evn de
monter: Espaces vectoriels normés
précédent: Notions de base
Emmanuel_Vieillard-Baron_pour_les.mathematiques