


monter: Espaces vectoriels normés
précédent: Propriétés des evn de
Soient (E, ) et (E,
) et (E, ') deux k-evn.
') deux k-evn.
On note 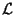 (E,F) l'ensemble des applications linéaires de E dans F et
(E,F) l'ensemble des applications linéaires de E dans F et 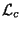 (E,F) l'ensemble des applications linéaires continues de E dans F.
(E,F) l'ensemble des applications linéaires continues de E dans F.
Théorème Soit
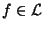 (E,F). Les affirmations suivantes sont équivalentes:
(E,F). Les affirmations suivantes sont équivalentes:
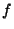 est élément de
est élément de 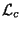 (E,F).
(E,F).
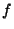 est continue en l'origine de E
est continue en l'origine de E .
.
- f est bornée sur la boule unitée de (E,
 ).
).
- f est lipschitzienne
 .
.
Démonstration Si 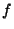 est élément de
est élément de 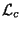 (E,F), il est claire que
(E,F), il est claire que 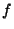 est continue en l'origine.
est continue en l'origine.
Supposons que 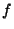 soit continue en l'origine et montrons qu'elle est bornée sur la sphère unité. La continuité en l'origine de
soit continue en l'origine et montrons qu'elle est bornée sur la sphère unité. La continuité en l'origine de 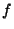 se traduit par :
se traduit par :
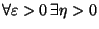
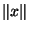 <
<
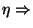
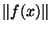
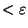
 .
Soit encore:
.
Soit encore:
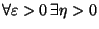
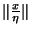 <
<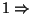
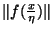
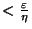 ce qui implique donc que si x
ce qui implique donc que si x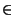
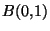 alors il existe un réél r tel que
alors il existe un réél r tel que 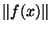 <r.
Si
<r.
Si 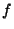 est bornée sur la boule unité par un réél strictement positif x, pour tout élément x de E,
est bornée sur la boule unité par un réél strictement positif x, pour tout élément x de E,
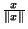 est élément de
est élément de 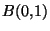 et
et
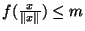 . Autrement écrit, Si x
. Autrement écrit, Si x 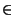 E,
E,
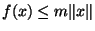 et f est bien Lipschitzienne
et f est bien Lipschitzienne .
Si f est Lipschitzienne sur E, il est claire que f est continue
.
Si f est Lipschitzienne sur E, il est claire que f est continue . On a alors prouvé le théorème.
. On a alors prouvé le théorème.
Proposition 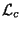 (E,F) a une structure de k-espace vectoriel.
(E,F) a une structure de k-espace vectoriel.
Démonstration Il suffit de vérifier 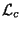 (E,F) est un sous espace vecoriel de
(E,F) est un sous espace vecoriel de 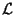 (E,F). Mais sachant qu'une somme d'application continue est continue
(E,F). Mais sachant qu'une somme d'application continue est continue , que l'application nulle est élément de
, que l'application nulle est élément de 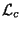 (E,F) et que la fonction produit d'un scalaire et d'une application continue est continue
(E,F) et que la fonction produit d'un scalaire et d'une application continue est continue , on vérifie les axiomes qui font de
, on vérifie les axiomes qui font de 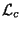 (E,F) un sous espace vectoriel de
(E,F) un sous espace vectoriel de 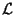 (E,F).
(E,F).
Si
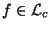 (E,F), on pose
(E,F), on pose
Proposition 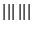 est une norme sur
est une norme sur 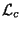 (E,F).
(E,F).
Démonstration Comme les éléments de 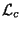 (E,F) sont bornés sur la sphère unité de E, il est claire que
(E,F) sont bornés sur la sphère unité de E, il est claire que
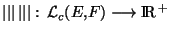 . Si une application linéaire continue vérifie
. Si une application linéaire continue vérifie 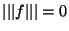 alors elle est nulle sur la boule unitée de E et donc, par homothétie, sur E tout entier. Réciproquement, l'application nulle vérifie
alors elle est nulle sur la boule unitée de E et donc, par homothétie, sur E tout entier. Réciproquement, l'application nulle vérifie 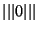 =0. Les deux axiomes qui restent à vérifier pour montrer que
=0. Les deux axiomes qui restent à vérifier pour montrer que 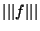 est une norme sont validés grâce au fait, justement, que
est une norme sont validés grâce au fait, justement, que  est une norme sur E.
est une norme sur E.
Conclusion (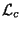 (E,F),
(E,F),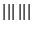 ) est un k-evn.
) est un k-evn.
Proposition Si E est de dimension finie, alors toute application linéaire de E dans F est continue.
Démonstration Si E est de dimension finie, alors toutes les normes sont équivalentes sur E . Considérons alors une base
. Considérons alors une base
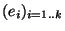 de E et si x=
de E et si x=
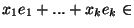 E, la norme sur E
E, la norme sur E 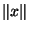 =
=
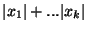 . On a alors
. On a alors 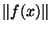 '=
'=
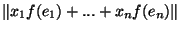 '
'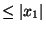
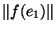 '+...
'+...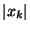
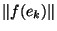 '. Posons M=
'. Posons M=
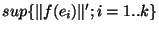 . Notre inégalité se réécrit:
. Notre inégalité se réécrit: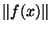 '
'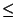 M
M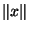 ce qui prouve la continuité de
ce qui prouve la continuité de 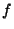 .
.
Terminons par une définition et un résultat supplémentaire à propos de (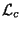 (E,F),
(E,F), ):
):
Définition Un espace vectoriel normé complet pour la métrique associée à sa norme est appellé un espace de Banach.
Lemme Si
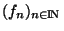 est de Cauchy
est de Cauchy  dans (
dans (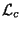 (E,F),
(E,F),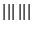 ) alors
) alors
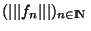 est bornée dans IR.
est bornée dans IR.
Définition Supposons que ce ne soit pas le cas. Alors pour tout n de IN, il existe 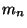 dans INet
dans INet 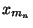 dans la boule unité fermé de E
dans la boule unité fermé de E  tels que
tels que
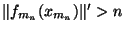 . Pour tout N dans INon peut alors trouver
. Pour tout N dans INon peut alors trouver 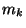 et
et 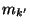 plus grands que N et tels que
plus grands que N et tels que
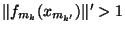 . La suite
. La suite
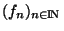 ne peut alors être de Cauchy. D'où le lemme par contradiction.
ne peut alors être de Cauchy. D'où le lemme par contradiction.
Proposition Si (F, ') est un espace de Banach alors il en est de même pour (
') est un espace de Banach alors il en est de même pour ( (E,F),
(E,F), ).
).
Démonstration Soit
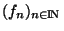 une suite de Cauchy
une suite de Cauchy  de (
de (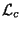 (E,F),
(E,F), ). Alors
). Alors
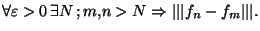 Mais si x est élément de E, on a
Mais si x est élément de E, on a
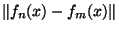 '
'
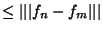
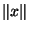 . Donc pour tout x de E,
. Donc pour tout x de E,
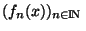 est de Cauchy. F étant complet pour sa norme
est de Cauchy. F étant complet pour sa norme , cette suite converge vers un élément
, cette suite converge vers un élément 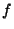 (x) de F
(x) de F . Cela nous permet de définir une application
. Cela nous permet de définir une application 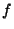 de E dans F.
de E dans F.
Montrons que l'application 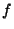 est le bon candidat pour la limite de
est le bon candidat pour la limite de
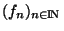 . Tout d'abord ,
. Tout d'abord , 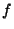 est linéaire: si x et y sont éléments de E,
est linéaire: si x et y sont éléments de E, 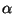 et
et 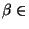 k alors:
k alors:
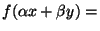
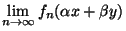 =
=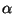
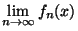 +
+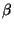
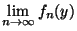 =
=
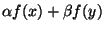 . Cqfd.
. Cqfd.
Montrons aussi que 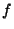 est continue: si x
est continue: si x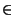
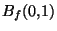
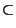 E alors:
E alors:
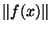 '
'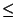
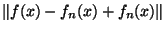 '
'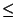
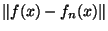 '+
'+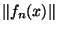 '
'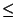 +
+
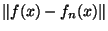 +
+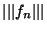 .
.
Donc
La quantité sup 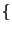
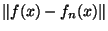 ;
;
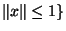 tend vers 0 quand n tend vers l'infini et d'après le lemme
tend vers 0 quand n tend vers l'infini et d'après le lemme , la suite
, la suite
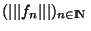 est bornée dans IR. Donc sup
est bornée dans IR. Donc sup 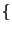
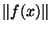 ;
;
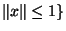 est bornée et
est bornée et 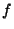 est continue sur E
est continue sur E .
Reste encore à montrer que
.
Reste encore à montrer que
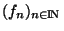 converge vers
converge vers 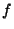 pour la norme
pour la norme 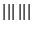 . Soit
. Soit 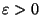 . Il existe N
. Il existe N 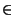 INtel que si p,q>N alors
INtel que si p,q>N alors
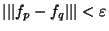 . Fixons x dans E On a alors
. Fixons x dans E On a alors
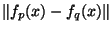 '
'
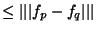
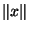
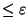
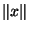 . Fixons p
. Fixons p 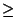 N et faisons tendre q vers l'infini. Cela donne:
N et faisons tendre q vers l'infini. Cela donne:
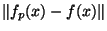 '
'
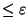
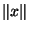 . Comme x est quelconque dans E, on peut écrire
. Comme x est quelconque dans E, on peut écrire
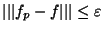 pour p>N, ce qui nous assure de la convergence de
pour p>N, ce qui nous assure de la convergence de
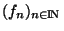 vers
vers 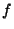 pour la norme
pour la norme  .
.



monter: Espaces vectoriels normés
précédent: Propriétés des evn de
Emmanuel_Vieillard-Baron_pour_les.mathematiques