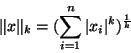suivant: Espaces vectoriels normés de
monter: Espaces vectoriels normés
précédent: Introduction
On considère dans tout ce chapitre un espace vectoriel réél ou complexe E. On notera k le corps de base. Donc k=IRou IC.
Définition
 est une norme sur E si:
est une norme sur E si:
 =0
=0
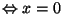 .
.
-
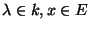
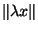 =|
=|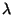 |
|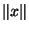 où | | désigne la valeurs absolue si k=IR
ou le module si k=IC.
où | | désigne la valeurs absolue si k=IR
ou le module si k=IC.
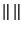 vérifie l'inégalité triangulaire:
vérifie l'inégalité triangulaire: 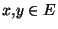
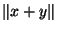
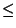
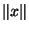 +
+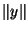 .
.
Proposition Si 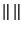 est une norme sur E alors |
est une norme sur E alors |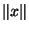 -
-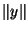 |
|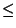
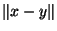 .
.
Démonstration A écrire!
Définition Un espace vectoriel normé est la donnée d'un espace vectoriel E et d'une norme 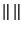 sur E. On notera (E,
sur E. On notera (E,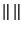 ) le couple formé par l'espace vectoriel et sa norme.
) le couple formé par l'espace vectoriel et sa norme.
Proposition fondamental Un evn est un espace métrique  : il suffit de poser, si x,y
: il suffit de poser, si x,y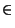 E, d(x,y)=
E, d(x,y)=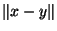 et d ainsi définie est une métrique
et d ainsi définie est une métrique . Cette métrique sera appelée métrique associée à la norme
. Cette métrique sera appelée métrique associée à la norme 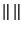 . Les espaces vectoriels normés sont donc des espaces métriques (et à fortioris des espaces topologiques
. Les espaces vectoriels normés sont donc des espaces métriques (et à fortioris des espaces topologiques ).
).
Exemple Quelques exemples d'evn :
Définition On dira que deux normes 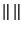
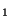 et
et 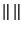
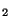 sont équivalentes si il existe
sont équivalentes si il existe
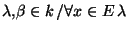
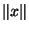
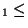
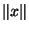
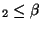
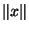
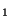 .
.
Proposition ``Etre équivalent à'' est une relation d'équivalence sur l'ensemble des normes d'un evn.
Démonstration Réflexivité, transitivité, symétrie....
Proposition Si deux normes sont équivalentes, les métriques corespondantes à ces deux normes sont aussi équivalentes.
Démonstration Ecrire!!!
Corollaire Si on a deux normes équivalentes sur un espace vectoriel donné alors les topologies inhérentes à ces deux normes sont équivalentes.
Démonstration Les normes sont équivalentes, donc les métriques associées le sont , et les topologies aussi
, et les topologies aussi .
.
Remarque fondamentale En fait c'est encore + fort que cela car la complètude  est conservée par changement de normes équivalentes. Ce qui n'est pas le cas par changement de topologie équivalente. Si, par exemple, une suite
est conservée par changement de normes équivalentes. Ce qui n'est pas le cas par changement de topologie équivalente. Si, par exemple, une suite
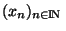 est de Cauchy
est de Cauchy  et qu'elle converge pour une norme donnée, il en sera de même pour tout autre norme équivalente.
et qu'elle converge pour une norme donnée, il en sera de même pour tout autre norme équivalente.
Proposition L'application norme
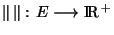 est continue
est continue  sur E muni de la topologie induite par
sur E muni de la topologie induite par 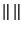
 . Elle est même 1-Lipschitzienne
. Elle est même 1-Lipschitzienne .
.
Démonstration Si x et y sont éléments de E, |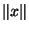 -
-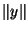 |
|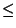
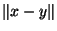 .
.
Proposition les homothéties vectorielles et les translations sont des applications continues  sur les evn.(Ce sont des isométries!!!).
sur les evn.(Ce sont des isométries!!!).
Démonstration Soit (E,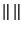 ) un evn ,soit
) un evn ,soit 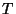 la translation de vecteur v et
la translation de vecteur v et 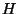 l'homothétie de rapport
l'homothétie de rapport 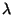 . On a donc, si x et y sont des éléments de E:
. On a donc, si x et y sont des éléments de E: 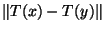 =
=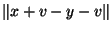 =
=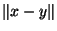 .
.  est donc 1-Lipschitzienne
est donc 1-Lipschitzienne  ce qui implique le résultat.
ce qui implique le résultat.
D'autre part 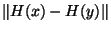 =
=
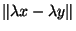 =
=
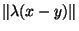 =|
=|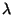 |
|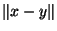 .
. 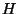 est alors
est alors 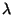 -Lipschitzienne
-Lipschitzienne .Cqfd car
.Cqfd car  .
.
Proposition Soit (X,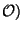 un espace topologique
un espace topologique  et (F,
et (F,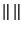 ) un evn. Notons
) un evn. Notons 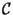 (X,F) l'ensemble des fonctions continues
(X,F) l'ensemble des fonctions continues  de X dans F alors
de X dans F alors 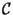 (X,F) est un espace vectoriel.
(X,F) est un espace vectoriel.
Démonstration Il suffit de montrer que 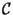 (X,F) est un sous espace vectoriel de l'espace des fonctions de X dans F. Il est tout d'abord clair que l'application nulle est élément de
(X,F) est un sous espace vectoriel de l'espace des fonctions de X dans F. Il est tout d'abord clair que l'application nulle est élément de 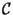 (X,F). Soient
(X,F). Soient 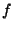 et
et 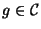 (X,F), soient aussi
(X,F), soient aussi 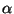 et
et 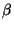 dans k. Il suffit de vérifier pour tout x de X, et tout
dans k. Il suffit de vérifier pour tout x de X, et tout 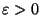 il existe V
il existe V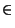
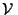 (x)
(x)  tel que
tel que

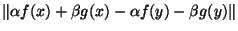 <
<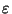
 . Fixons donc
. Fixons donc 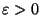 et x
et x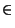 X. Comme f et g sont continues en x, on peut trouver des voisinages
X. Comme f et g sont continues en x, on peut trouver des voisinages 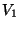 et
et 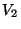 de x
de x  tels que
tels que
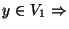
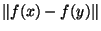 <
<
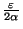 et
et
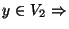
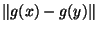 <
<
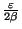 . En choisissant pour V le voisinage de x:
. En choisissant pour V le voisinage de x: 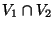 et en appliquant l'inégalité triangulaire
et en appliquant l'inégalité triangulaire  à
à
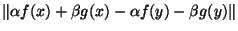 , on montre l'inégalité voulue. Comme x est quelconque dans X, on a bien prouvé que
, on montre l'inégalité voulue. Comme x est quelconque dans X, on a bien prouvé que
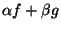 est continue sur X
est continue sur X .
.
En a en particulier ici prouvé le corollaire suivant:
Corollaire
- Une somme d'application continue est continue
 .
.
- L'application définie comme le produit d'un scalaire et d'une fonction continue est continue.



suivant: Espaces vectoriels normés de
monter: Espaces vectoriels normés
précédent: Introduction
Emmanuel_Vieillard-Baron_pour_les.mathematiques