suivant: Notions de base
monter: Espaces vectoriels normés
précédent: Espaces vectoriels normés
Les espaces vectoriels normés (evn) sont des espaces métriques particuliers mais d'une importance capitale en analyse. Ainsi, le calcul différentiel a pour théatre les espaces de Banach 
qui sont des evn particuliers. D'autre part, beaucoups de résultats d'analyse fonctionnelle ont comme terrain d'appuis les espaces Hilbertiens, qui sont eux aussi des evn.
Par ailleurs, un résultat propre , aux evn qui sont de dimension finie:l'équivalence des normes, a pour conséquence que tout les evn de même dimension (sur um même corps de base) sont homéomorphes. Il suffira de connaître alors les propriétés topologiques de k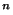
, où k désigne le corps de base de notre espace vectoriel E et n sa dimension, pour tout savoir de la topologie de E.
Emmanuel_Vieillard-Baron_pour_les.mathematiques