suivant: Théorèmes de Sylows
monter: Théorème de Cauchy et
précédent: Introduction
Théorème de Cauchy
Soit (G,.) un groupe fini et p un diviseur premier de l'ordre de G. Alors il existe un élément d'ordre p
et p un diviseur premier de l'ordre de G. Alors il existe un élément d'ordre p dans G.
dans G.
Démonstration Soit p un diviseur premier de |G|. Considérons l'ensemble
où e désigne le neutre de G. Pour choisir un élément x de X, nous devons faire p-1 choix d'éléments dans G, donc le cardinal de X est |G|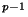 . On fait agir
. On fait agir
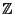 /p
/p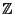 sur X de la façon suivante: (On commettra sans aucun scrupule l'abus de notation qui consiste à identifier la classe d'équivalence de i
sur X de la façon suivante: (On commettra sans aucun scrupule l'abus de notation qui consiste à identifier la classe d'équivalence de i
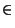
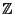 et l'élément de
et l'élément de 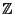 compris entre 0 et p-1 qui est un représentant
compris entre 0 et p-1 qui est un représentant de cette classe d'équivalence. Autrement dit, on ne sera pas gêné par l'égalité
de cette classe d'équivalence. Autrement dit, on ne sera pas gêné par l'égalité 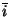 =k où k est le représentant de
=k où k est le représentant de 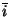 qui est compris entre 0 (compris) et p (non compris)). Si x est l'élément (x
qui est compris entre 0 (compris) et p (non compris)). Si x est l'élément (x ,...,x
,...,x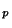 ) de X et si
) de X et si 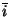 est la classe d'équivalence de i (0
est la classe d'équivalence de i (0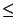 i<p) dans
i<p) dans 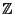 /p
/p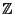 , alors
, alors 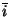 .x=(x
.x=(x
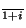 ,...,x
,...,x
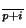 ). On vérifie sans peine que ceci définit bien une action
). On vérifie sans peine que ceci définit bien une action sur X. Supposons que G ne possède aucun élément d'ordre p
sur X. Supposons que G ne possède aucun élément d'ordre p .
.
Remarquons que l'orbite de (e,...,e)
de (e,...,e)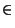 X n'a qu'un élément. Si un autre élément x de X n'a que lui même dans son orbite, alors en particulier, x=(x
X n'a qu'un élément. Si un autre élément x de X n'a que lui même dans son orbite, alors en particulier, x=(x
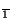 ,...,x
,...,x
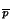 )= (x
)= (x
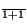 ,...,x
,...,x
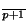 )=(x
)=(x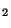 ,...,x
,...,x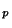 ,x
,x )=(x
)=(x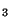 ,...,x
,...,x ,x
,x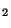 )=... . Et donc x
)=... . Et donc x =x
=x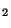 =...=x
=...=x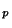 et x
et x
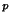 =e, ce qui implique que G possède un élément x
=e, ce qui implique que G possède un élément x d'ordre p et est contraire à notre hypothèse de départ. On suppose donc que (e,...,e) est le seul élément de X possèdant une orbite ne contenant que lui même. Si x est un élément de X, |w(x)| est alors un diviseur de |
d'ordre p et est contraire à notre hypothèse de départ. On suppose donc que (e,...,e) est le seul élément de X possèdant une orbite ne contenant que lui même. Si x est un élément de X, |w(x)| est alors un diviseur de |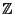 /p
/p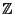 |=p différent de 1. Comme p est premier, ceci implique que |w(x)|=1. Choisissons alors des éléments x de X dont les orbites respectives partitionnent X. La formule des classes
|=p différent de 1. Comme p est premier, ceci implique que |w(x)|=1. Choisissons alors des éléments x de X dont les orbites respectives partitionnent X. La formule des classes nous donne:
nous donne:
Donc |X| est de la forme 1+m.p où m désigne le nombre d'orbites de taille plus grande que 1 et partitionnant X. Ceci contredit le fait que |X| est de cardinal |G|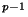 qui est divisible par p. Nous venons alors de démontrer par l'absurde que G possèdait au moins un élément d'ordre p
qui est divisible par p. Nous venons alors de démontrer par l'absurde que G possèdait au moins un élément d'ordre p .
.



suivant: Théorèmes de Sylows
monter: Théorème de Cauchy et
précédent: Introduction
Emmanuel_Vieillard-Baron_pour_les.mathematiques
![]() et p un diviseur premier de l'ordre de G. Alors il existe un élément d'ordre p
et p un diviseur premier de l'ordre de G. Alors il existe un élément d'ordre p![]() dans G.
dans G.