


suivant: Intérieur et adhérence d'un
monter: Espaces métriques
précédent: Métrique induite
Définition
Rappelons qu'une suite est un ensemble de points indexés par les éléments de INdans X. Soit
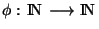 une application croissante. L'ensemble de points
une application croissante. L'ensemble de points
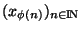 est encore un ensemble de points indexés par INet est appelé suite extraite ou sous suite de la suite
est encore un ensemble de points indexés par INet est appelé suite extraite ou sous suite de la suite
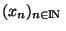 .
.
Définition
On appelera valeur d'adhérence de la suite
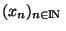 tout élément x de X tel que
tout élément x de X tel que
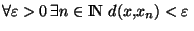 .
.
Remarque x est valeur d'adhérence de la suite
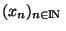 si et seulement si, pour tout voisinage V de x, il existe n dans INtel que x
si et seulement si, pour tout voisinage V de x, il existe n dans INtel que x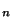 soit élément de V.
soit élément de V.
Remarque Tout élément de
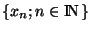 est valeur d'adhérence de
est valeur d'adhérence de
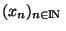 .
.
Définition
On appelera point d'accumulation de la suite
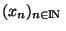 toute valeur d'adhérence x de cette suite qui n'est pas un élément de
toute valeur d'adhérence x de cette suite qui n'est pas un élément de
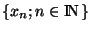 .
.
Définition
On dira que la suite
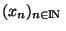 d'éléments de X converge vers l'élément x de X si:
d'éléments de X converge vers l'élément x de X si:
Définition
x est la limite de
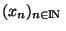 quand n tend vers l'infini. On écrira:
quand n tend vers l'infini. On écrira:
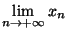 =x
=x
Remarque Si x est limite de la suite
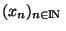 alors c'est l'unique point d'accumulation de cette suite.
alors c'est l'unique point d'accumulation de cette suite.
Proposition
On a équivalence entre
- x est valeur d'adhérence de la suite
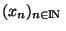 .
.
- Il existe une suite extraite de la suite
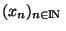 qui converge vers x.
qui converge vers x.

Démonstration Supposons que x soit valeur d'adhérence  de
de
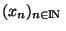 . Si x est élément de
. Si x est élément de
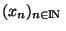 alors il existe
alors il existe
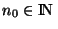 tel que x=
tel que x=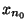 et on pose, pour tout n dans IN,
et on pose, pour tout n dans IN, 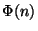 =
=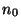 . La sous suite
. La sous suite 
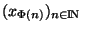 converge
converge  alors clairement vers x. Si x n'est pas élément de la suite ( c'est donc un point point d'accumulation
alors clairement vers x. Si x n'est pas élément de la suite ( c'est donc un point point d'accumulation ), on peut trouver m dans INtel que x
), on peut trouver m dans INtel que x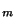 soit élément de
soit élément de 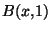
 . On pose
. On pose 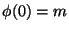 . Supposons construit jusqu'à l'ordre N une application
. Supposons construit jusqu'à l'ordre N une application
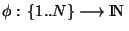 croissante et une suite
croissante et une suite
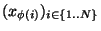 telle que pour tout i
telle que pour tout i
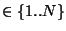 , x
, x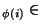
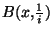 . Construisons l'élément x
. Construisons l'élément x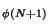 . Considérons pour cela la boule
. Considérons pour cela la boule
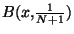
 . Cette boule est bien entendue un voisinage ouvert
. Cette boule est bien entendue un voisinage ouvert  de x. Supposons que l'ensemble
de x. Supposons que l'ensemble
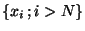 n'intersecte pas cette boule. Alors on pourrait facilement construire un voisinage de x qui n'intersecte pas
n'intersecte pas cette boule. Alors on pourrait facilement construire un voisinage de x qui n'intersecte pas
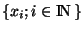 . Ce qui impliquerait que x n'est pas valeur d'adhérence
. Ce qui impliquerait que x n'est pas valeur d'adhérence  de
de
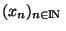 et qui est contraire à notre hypothèse de départ. L'ensemble
et qui est contraire à notre hypothèse de départ. L'ensemble
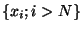 intersecte donc
intersecte donc
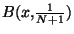 en un ensemble non vide. Soit x
en un ensemble non vide. Soit x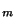 un point de cette intersection. On a, par construction, m>N. Posons
un point de cette intersection. On a, par construction, m>N. Posons 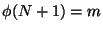 . On a bien
. On a bien
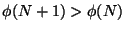 et x
et x
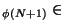
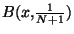 . On construit ainsi notre suite
. On construit ainsi notre suite
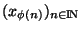 par récurrence.
par récurrence.
Il faut encore montrer qu'elle converge vers x. Choisissons donc 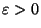 . Comme la suite
. Comme la suite
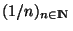 converge vers 0
converge vers 0  , pour N assez grand, on peut supposer que si n>N alors 1/n<
, pour N assez grand, on peut supposer que si n>N alors 1/n<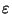 . Mais alors, si n>N, on a, par construction de
. Mais alors, si n>N, on a, par construction de
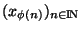 , x
, x
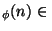
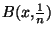
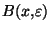 . Donc, si n>N, d(x
. Donc, si n>N, d(x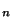 ,x)<
,x)<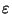 , Cqfd
, Cqfd  .
.



suivant: Intérieur et adhérence d'un
monter: Espaces métriques
précédent: Métrique induite
Emmanuel_Vieillard-Baron_pour_les.mathematiques