suivant: Métrique induite monter: Espaces métriques précédent: Notions de base

Sous ensembles ouverts et sous ensembles fermés

Définition Un sous ensemble U de X sera dit ouvert si il est vide ou si pour tout élément x de cet ensemble on peut trouver une boule ouverte de rayon suffisamment petit en sorte qu'elle soit toute entière contenue dans U.
Définition L'ensemble 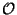$\cal O$ de tous les ouverts de X s'appelle la topologie

de X.
Proposition

X est ouvert.
Une réunion quelconque d'ensemble ouverts est ouverte
Une intersection finie d'ensembles ouverts est ouverte.

Démonstration Contentons nous de prouver le cas de l'intersection. Les deux autres cas sont absoluments triviaux.
Soit n 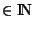$\in {\rm I\!N }$ . On considère une famille de n ensembles ouverts

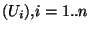. Soit x un point dans l'intersection de ces n ensembles. x est donc un point de chacun de ces ouverts. On peut alors trouver, pour tout i=1..n un réél

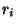tel que la boule de centre

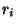et de centre x

soit incluse dans

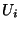. Posons 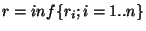$r=inf \lbrace r_i;i=1..n \rbrace$ . La boule

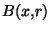est alors contenue dans chacun des

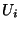et on a ainsi trouvé une boule ouverte centrée en x et contenue dans l'intersection des

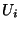. Cette intersection est donc bien ouverte.
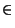
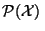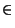Définition Soit V $\in$ $\cal{P(X)}$ et x $\in$ X On dira que V est un voisinage de x si il existe un ouvert U de X tel que x soit élément de U et U soit inclus dans V

.
On notera 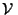$\cal{V}$ (x) l'ensemble de tous les voisinages de x.
Proposition

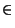
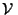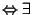
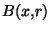
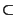V $\in$ $\cal{V}$ (x) $\Leftrightarrow \exists$ $\subset$ V.
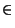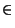
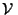Si O est ouvert dans X et si x $\in$ O alors O $\in$ $\cal{V}$ (x)

Proposition Un sous ensemble O de X est ouvert si et seulement si il est voisinage de chacun de ses points.
Démonstration D'après la remarque précédente, le sens direct est évident. Montrons la réciproque. Supposons donc que O est un ensemble qui est voisinage de chacun de ses points. Pour tout x dans O, on peut donc trouver un sous ensemble O(x) de O tel que O(x) soit ouvert. On peut même écrire:

$\begin{displaymath}O=\bigcup_{x \in O}O(x).\end{displaymath}$

O est donc réunion quelconque d'ouverts

. Ceci implique évidemment que O est ouvert.
Définition Le complémentaire d'un sous ensemble ouvert de X sera appelé sous ensemble fermé.
Proposition

X et 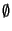$\emptyset$ sont fermés.
Une réunion finie de fermés est fermée.
Une intersection quelconque de fermés est fermée.

Démonstration C'est trivial, via les égalités suivantes (A et B désigne deux ensembles quelconques):

$\begin{displaymath}(A \bigcup B)^c=A^c \bigcap B^c et (A \bigcap B)^c=A^c \bigcup B^c\end{displaymath}$

suivant: Métrique induite monter: Espaces métriques précédent: Notions de base

Emmanuel_Vieillard-Baron_pour_les.mathematiques