


suivant: Notions supplémentaires sur les
monter: Groupes
précédent: Sous groupe d'un groupe
On considère dans ce paragraphe deux groupes (G,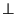 ) et (H,
) et (H,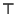 ). On note
). On note 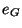 et
et 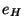 les neutres respectifs de G et H. (
les neutres respectifs de G et H. (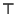 se
prononce truc).
se
prononce truc).
Définition On dit qu'une application
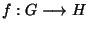 est un homomorphisme de groupe si:
est un homomorphisme de groupe si:
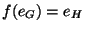 .
.
- Si x et y sont éléments de G,
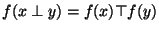 .
.
De plus:
- Si G=H, nous dirons que
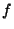 est un endomorphisme.
est un endomorphisme.
- Si
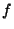 est bijective, nous dirons que f est un isomorphisme. Si il existe un isomorphisme entre G et H, nous dirons que G et H sont
isomorphes et nous noterons G
est bijective, nous dirons que f est un isomorphisme. Si il existe un isomorphisme entre G et H, nous dirons que G et H sont
isomorphes et nous noterons G H.
H.
- Si
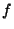 est à la fois un isomorphisme et un endomorphisme, nous dirons que
est à la fois un isomorphisme et un endomorphisme, nous dirons que 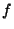 est un automorphisme.
est un automorphisme.
Remarque La notion d'isomorphisme joue en algèbre un rôle dual à celui des homéomorphismes en topologie  ou des difféomorphismes en géométrie
différentielle. Des groupes qui seront isomorphes auront les mêmes propriétés algébriques. Ainsi, l'étude algébrique d'un groupe pourra se faire sur
n'importe quel groupe qui lui est isomorphe.
ou des difféomorphismes en géométrie
différentielle. Des groupes qui seront isomorphes auront les mêmes propriétés algébriques. Ainsi, l'étude algébrique d'un groupe pourra se faire sur
n'importe quel groupe qui lui est isomorphe.
Proposition  Soit x un élément de G,
Soit x un élément de G,
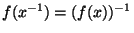 .
.
Démonstration Choisissons x dans G. On a
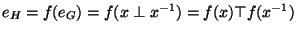 et donc par définition de l'inverse d'un élément d'un groupe,
et donc par définition de l'inverse d'un élément d'un groupe,
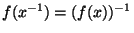
 .
.
Définition  Soit f un homomorphisme de G dans H. Nous noterons
Soit f un homomorphisme de G dans H. Nous noterons 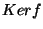 ou
ou 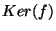 l'ensemble
l'ensemble
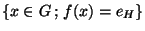 . Cet ensemble s'appelle le
noyau de l'homomorphisme f.
. Cet ensemble s'appelle le
noyau de l'homomorphisme f.
Remarque En allemand, noyau se dit Kernel.
Remarque Le noyau d'un homomorphisme n'est jamais vide. En effet, le neutre du groupe de départ est toujours élément du noyau.
Théorème Soit f un homomorphisme entre G et H. On a équivalence entre:
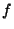 est injective.
est injective.
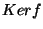 est réduit à l'élément neutre de G.
est réduit à l'élément neutre de G.
Démonstration Si 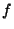 est injective, l'image du neutre de G par
est injective, l'image du neutre de G par 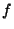 étant le neutre de H, aucun autre élément de G ne peut avoir
étant le neutre de H, aucun autre élément de G ne peut avoir 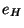 comme image. ( Ou sinon
cela contredit l'injectivité de
comme image. ( Ou sinon
cela contredit l'injectivité de 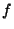 ). Donc le noyau de
). Donc le noyau de 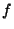 se réduit à
se réduit à
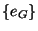 .
.
Si cette dernière propriété est vérifiée, prenons x et y dans G telles que 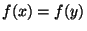 . Alors
. Alors 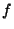 étant un homomorphisme,
étant un homomorphisme,
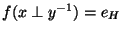 .
Donc
.
Donc
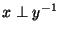 est élément de
est élément de 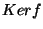 . Mais le noyau de
. Mais le noyau de 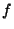 étant réduit à
étant réduit à
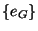 , cela implique que
, cela implique que
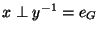 et
donc que
et
donc que 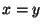 .
.
Proposition Soit
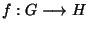 un homomorphisme . Alors:
un homomorphisme . Alors:
- Ker f est un sous groupe de G
 .
.
- Im f (= l'image de f=
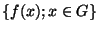 ) est un sous groupe de H
) est un sous groupe de H .
.

Démonstration Montrons que le noyau de 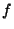 est un sous groupe de G.
est un sous groupe de G. 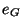 est naturellement élément de Ker
est naturellement élément de Ker 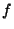 . Soient x et y des éléments de Ker
. Soient x et y des éléments de Ker 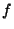 . Alors
. Alors
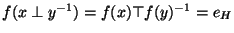 . Ceci prouve que
. Ceci prouve que 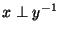 est élément de Ker
est élément de Ker 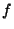
 .
.
Montrons maintenant que Im 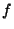 est un sous groupe de H. Remarquons que
est un sous groupe de H. Remarquons que 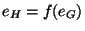 et donc que
et donc que 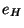 est élément de Im
est élément de Im 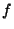 . Soient encore
. Soient encore 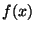 et
et
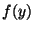 des éléments de Im
des éléments de Im 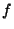 . Alors
. Alors
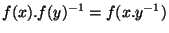 est bien élément de Im
est bien élément de Im 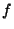
 .C.q.f.d.
.C.q.f.d.
Proposition L'application composée de deux homomorphismes est encore un homomorphisme.
Démonstration Triviale!!!



suivant: Notions supplémentaires sur les
monter: Groupes
précédent: Sous groupe d'un groupe
Emmanuel_Vieillard-Baron_pour_les.mathematiques