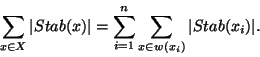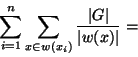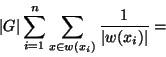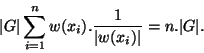monter: Action de groupe précédent: Définition

Propriétés

Dans tout ce paragraphe on s'intéresse à un groupe G agissant sur un ensemble X via une action $\theta$ .

Proposition La relation sur X définie par : si x, y $\in$ X,x $\sim$ y $\Leftrightarrow$ y $\in$ w(x) est une relation d'équivalence sur X.

Démonstration Comme d'habitude réflexitivité, symétrie, transitivité...

Remarque Les actions de groupes nous permettront donc de partitionner des ensembles suivant des classes d'équivalence.

Proposition Si x est élément de X alors Stab(x) est un sous groupe de G.

Démonstration Remarquons que e est toujours élément de stab(x). Remarquons aussi que si g $\in$ Stab(x) alors x=e.x=(g $^{-1}$ .g).x=(g $^{-1}$ .(g.x))=g $^{-1}$ .x. Donc g $^{-1}$ est élément de Stab(x). Soient maintenant g,g' $\in$ Stab(x), alors on vérifie facilement que g.g' $^{-1}\in$ Stab(x).

Proposition Si x et y $\in$ X sont éléments d'une même orbite alors stab(x) et stab(y) sont des sous groupes conjugués de G.

Démonstration Comme x et y sont dans une même orbite, il existe h $\in$ G tel que h.x=y. Mais alors si g $\in$ Stab(x), h.g.h $^{-1}\in$ Stab(y): h.g.h $^{-1}$ .y=h.g.x=h.x=y. Donc h.Stab(x).h $^{-1}\subset$ Stab(y). On montrerait de même que h $^{-1}$ .Stab(y).h $\subset$ Stab(x), Ce qui nous prouve que h.Stab(x).h $^{-1}$ =Stab(y) et que ces deux sous groupes sont conjugués.

Proposition Soit x $\in$ X. On a une bijection entre G/stab(x) et w(x).

Démonstration Afin de le démontrer cela nous allons définir une application G/Stab(x) $\longrightarrow$ w(x) par : si $\overline{g}\in$ G/Stab(x) alors (x)=g.x.
Montrons que est bien définie: si g et g' sont des représentants de $\overline{g}$ alors il existe h $\in$ Stab(x) tel que g'=g.h. Donc g'.x=g.h.x=g.x. ne dépend donc pas du représentant de $\overline{g}$ choisie et est donc bien définie.
Montrons que est injective: Si g.x=g'.y alors g' $^{-1}$ .g est élément de Stab(x). Autrement dit $\overline{g'^{-1}.g}=\overline{e}$ et $\overline{g}=\overline{g'}$ . est donc injective.
est surjective: Si y $\in$ w(x) alors par définition de w(x), il existe g $\in$ G tel que g.x=y. Donc (g)=y.
La proposition est maintenant démontrée.

Corollaire Si G est fini, ${\vert G\vert}\over{\vert Stab(x)\vert}$ = $\vert w(x)\vert$ . (Si A est un ensemble |A| désigne le cardinal de A).

Démonstration C'est immédiat par application du théorème de Lagrange.

Proposition On suppose que G est fini. Soit $\lbrace x_i; i=1,..,n \rbrace$ un sous ensemble d'éléments de X tel que $\lbrace w(x_i);i=1,...,n \rbrace$ est une partition de X. Alors

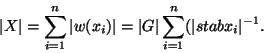
$\begin{displaymath}\vert X\vert=\displaystyle{\sum_{i=1}^n \vert w(x_i)\vert=\vert G\vert\sum_{i=1}^n (\vert stab{x_i}\vert^{-1}}.\end{displaymath}$

Théorème Formule de la moyenne On suppose G de cardinal fini et agissant sur un ensemble X. Alors si n désigne le nombre d'orbites distinctes de l'action,si $\cal A$ désigne le sous ensemble de X composé d'un représentant pour chacune de ces orbites, on a:

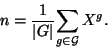
$\begin{displaymath}n={{1}\over{\vert G\vert}}\displaystyle{\sum_{g\in \cal G}X^g}.\end{displaymath}$

Démonstration Considérons un sous ensemble $\cal A$ de X comme dans l'énoncé du théorème. Nous allons nous intéresser à l'ensemble G $\times$ X, et plus précisément au sous ensemble $\cal O$ de ce dernier définit par ${\cal O}=\lbrace (g,x)\in G\times X;g.x=x\rbrace$ . On a

$\begin{displaymath}{\cal O}=\displaystyle{\bigcup_{g\in G} Fix(g)=\bigcup_{x\in X} Stab(x)} .\end{displaymath}$

Ceci nous donne:

$\begin{displaymath}\displaystyle{\sum_{g\in G} \vert Fix(g)\vert=\sum_{x\in X} \vert Stab(x)\vert} .\end{displaymath}$

On a aussi:

$\begin{displaymath}\displaystyle{\sum_{x\in X} \vert Stab(x)\vert=\sum_{i=1}^n\sum_{x\in w(x_i)} \vert Stab(x_i)\vert} .\end{displaymath}$

Mais pour tout x $\in$ X, |stab(x)|.|w(x)|=|G|

. Donc

$\begin{displaymath}\displaystyle{\sum_{x\in X} \vert Stab(x)\vert}=\end{displaymath}$

$\begin{displaymath}\displaystyle{\sum_{i=1}^n\sum_{x\in w(x_i)} {\vert G\vert\over \vert w(x)\vert}}=\end{displaymath}$

$\begin{displaymath}\displaystyle{\vert G\vert\sum_{i=1}^n\sum_{x\in w(x_i)} {1\over \vert w(x_i)\vert}}=\end{displaymath}$

$\begin{displaymath}\displaystyle{\vert G\vert\sum_{i=1}^n w(x_i).{1\over \vert w(x_i)\vert}}=n.\vert G\vert .\end{displaymath}$

En divisant par |G| les deux membres de notre égalité, on obtient la formule voulue.

monter: Action de groupe précédent: Définition

Emmanuel_Vieillard-Baron_pour_les.mathematiques