next up previous
monter: Espaces métriques connexes précédent: Application continue sur un

Quelques critères de connexité

Proposition Si un sous ensemble U de X est connexe, il en est de même de son adhérence.
Démonstration Soit

\begin{displaymath}f:{\overline U} \longrightarrow \lbrace 0,1 \rbrace\end{displaymath}

une application continue. (L'adhérence de U est munie de la topologie induite de celle de X et $\lbrace 0,1 \rbrace$ est muni de la topologie discrète ). $f$ est donc continue sur U. Mais U étant connexe, ceci implique que $f$ est constante sur U. On peut par exemple supposer que $f$ vaut 1 sur U. Soit x un élément de

\begin{displaymath}{\overline U}\setminus U .\end{displaymath}

Supposons que $f$(x)=0. Comme $f$ est continue et que $\lbrace 0 \rbrace$ est un ouvert de $\lbrace 0,1 \rbrace$ muni de la topologie discrète,$f^{-1}$(0) est un ouvert de l'adhérence de U contenant x. C'est donc, en particulier, un voisinage de x . Mais comme x est adhérent à U , ce voisinage intersecte nécessairement U, et donc, par construction de ce voisinage, U possède des points dont l'image par $f$ est nulle. Ce qui est absurde, par hypothèse. Donc $f\equiv 1$ sur l'adhérence de U et cette adhérence est donc belle et bien connexe. Cqfd.
Proposition Soient $(U_i)_{\scriptsize {i \in I}}$ une famille de sous ensembles connexes de X tels $\displaystyle{\bigcap_{i\in I} U_i \neq \emptyset}$ Alors: $\displaystyle{\bigcup_{i\in I} U_i}$ est connexe.
Démonstration Notons U la réunion des $(U_i)_{\scriptsize {i \in I}}$ et supposons qu'il existe une application continue $f: U\longrightarrow \lbrace 0,1\rbrace$. Soit $a \in X$ un point de l'intersection des $(U_i)_{\scriptsize {i \in I}}$. La restriction de $f$ à $U_i$, i étant fixé dans I, est encore une application continue à valeurs dans $\lbrace 0,1 \rbrace$. Comme $U_i$ est connexe, il s'en suit que f est constante sur $U_i$. On peut supposer, par exemple, que $f$ vaut 0 sur $U_i$. On aura donc $f(a)=0$. i étant quelconque dans I, f est alors constante sur chaque $U_i, \forall i \in I$. Mais l'égalité $f(a)=0$ implique que $f$ est nulle sur tout $U_i, \forall i \in I$ et donc que $f$ est nulle sur U et donc constante sur U. Ce qui implique que U est connexe. Cqfd.
Définition Soit x un élément de X. On appelle composante connexe de x la réunion des sous ensembles connexes de X contenant x.
Proposition Soit x un élément de X. $ $
Démonstration La première partie de la proposition est évidente, par définition de la composante connexe d'un point . La seconde partie s'en déduit aussitôt car, rappelons-le, si un ensemble est connexe il en est de même de son adhérence qui de plus est fermée . Donc si U est le plus grand connexe de X contenant x, il est nécessairement égale à son adhérence qui est aussi connexe et qui contient aussi x.
Proposition Soit $((X_i,d_i))_{\scriptsize {i \in I}}$ une famille d'espaces métriques connexes. Alors Z, l'espace produit des $X_i$ est connexe pour la métrique produit .
Démonstration Soient 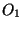$O_1$ et $O_2$ deux ouverts de Z non vides et partitionnants Z. Fixons $i\in I$ et notons $\Pi_i$ le projecteur de Z sur $X_i$ . On a: $X_i=\Pi_i(Z)=\Pi_i(O_1) \cup \Pi_i(O_2)$ et $\Pi_i(O_1) \cap \Pi_i(O_2)=\emptyset$. Les projecteurs étant des applications ouvertes , $\Pi_i(O_1)$ et $\Pi_i(O_2)$ sont des ouverts de $X_i$. Ils définissent donc une partition de $X_i$ en deux ouverts disjoints. 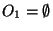Mais $X_i$ étant connexe, cela implique, par exemple, que $\Pi_i(O_1)=\emptyset$ et $\Pi_i(O_2)=X_i$. Cela implique par ailleurs que $O_1=\emptyset$ et $O_2=Z$ et que Z est connexe.
Réciproquement, les projecteurs $\Pi_i$ étant continues sur Z pour la métrique produit et la topologie de $X_i$ , si l'on suppose que Z est connexe, il en est de même de $X_i$ .
Corollaire ICmuni de l'une quelconque de ses normes est connexe comme produit de IRpar lui même.
Corollaire IR$^n$ muni de l'une quelconque de ses normes est connexe.
Définition Soient x et y deux éléments de X. On appelle chemin d'extrémités x et y (ou chemin joignant x et y de X toute application continue $c: [0,1]\longrightarrow X$ telle que $c(0)=x$ et $c(1)=y$.
Définition On dira que (X,${\cal O)}$ est connexe par arc si tout couple d'éléments de X peut être joint par un chemin.
Proposition Si X est connexe par arc alors X est connexe.
Démonstration Supposons donc que X n'est pas connexe. Soit alors $\lbrace U ,V \rbrace$, une partition de X en deux fermés. Soient aussi x un élément de U et y un élément de V. Comme X est connexe par arc, il existe un chemin $c: [0,1]\longrightarrow X$ telle que $c(0)=x$ et $c(1)=y$. Notons $A=\lbrace t \in [0,1] / c(t) \in U \rbrace$. Comme $A$ est un sous ensemble majoré de IR, il possède une borne supérieur que l'on note $t_0$. Notons, d'autre part, $B=\lbrace t \in [0,1] / c(t) \in V \rbrace$. $B$ est un sous ensemble minoré de IRet possède, par conséquent,une borne inférieure que l'on note $t_1$. 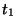On a nécessairent $t_0 = t_1$. Supposons que ce ne soit pas le cas, alors $t_0 < t_1$. On peut alors trouver un réél t élément de $]t_0,t_1[$. Mais l'élément c(t) de X ne peut alors ni être élément de U, ni de V. Ce qui est impossible. Notons $T=t_0=t_1$
$T$ étant la borne supérieure de $A$, on peut construire une suite $(t_n)_{\scriptsize {n \in {\rm I\!N }}}$ d'éléments de $A$ convergeante vers $T$. Mais U étant fermé et c continue , $\displaystyle{\lim_{n\rightarrow \infty}c(t_n)}$=c($T$) est élément de U. De même, on montrerait que c($T$) est élément de V. Mais U et V ont été supposés disjoints. On aboutit alors à une contradiction et X est bien connexe.
Remarque Attention, la réciproque est fausse.
next up previous
monter: Espaces métriques connexes précédent: Application continue sur un
Emmanuel_Vieillard-Baron_pour_les.mathematiques